Research Article
Volume 2 Issue 5 - 2018
Global Workspace, Self, and Mathematical Intuition
Dubník, Slovakia, Analyst-researcher
*Corresponding Author: Robert Skopec, Dubník, Slovakia, Analyst-researcher.
Received: June 06, 2018; Published: July 28, 2018
Abstract
In human consciousness a world of separated objects is perceived by an inner observer as a feeling of One-self. A topological correlation of the Self to the world, by either emerging all separated objects into one or splitting the Self in as many disconnected Sub-selves as there are objects perceived. The Self is generated in a neural network by algorithmic compression of spatial and temporal information into a toponeuronal structure (TNS). A correlation of an inner observer to parts of a structure inevitably entails a correlation to the whole, serving of the Self. Molecular mechanisms for the generation of a TNS in a neural network will be discussed.
Coding of reward probability and uncertainty by dopamine neurons
The brain continuously makes predictions and compares outcomes (or inputs) with those predictions. Predictions are fundamentally concerned with probability. Substantial evidence indicates that dopamine neurons of the primate ventral midbrain code errors in the prediction of reward. Dopamine neurons of ventral midbrain areas A8, A9, and A10 were identified solely on the basis of electropfysiological characteristics, particularly the long waveform of their impulses (1.5 to 5.0 ms). The phasic activations varied monotonically with reward probability. Statistical analysis revealed a significant effect of uncertainty on the population response (P < 0.005 in each of four data sets) indicating that the sustained activation codes uncertainty. The peak of sustained activation occurs at the time of potential reward, which corresponds to the moment of greatest uncertainty [1].
The brain continuously makes predictions and compares outcomes (or inputs) with those predictions. Predictions are fundamentally concerned with probability. Substantial evidence indicates that dopamine neurons of the primate ventral midbrain code errors in the prediction of reward. Dopamine neurons of ventral midbrain areas A8, A9, and A10 were identified solely on the basis of electropfysiological characteristics, particularly the long waveform of their impulses (1.5 to 5.0 ms). The phasic activations varied monotonically with reward probability. Statistical analysis revealed a significant effect of uncertainty on the population response (P < 0.005 in each of four data sets) indicating that the sustained activation codes uncertainty. The peak of sustained activation occurs at the time of potential reward, which corresponds to the moment of greatest uncertainty [1].
The uncertainty is signaled by dopamine neurons, and the common measures of uncertainty (variance, standard deviation, and entropy) are all maximal at P = 0.5, having highly nonlinear relations to probability, being very sensitive to small changes in probability near the extremes (P = 0 or 1). By always coding prediction error over the full range of probabilities, dopamine neurons could provide a teaching signal in accord with the principles of learning. The goal of learning can be seen as finding accurate predictors for motivationally significant events.
As indicated by mathematical principles of Shannon information, only in the presence of uncertainty is it anticipated that there will be information available in the outcome. When the prediction of reward is uncertain, the outcome (reward or no reward) always contains information. The outcome at P = 0.5 contains, on average, the maximal amount of information (one bit) of any probability. The responses of dopamine neurons multiplicatively combine the probability and magnitude of reward.
The error-likelihood model of Global Workspace
Such techniques as functional magnetic resonance imaging (fMRI) and electrical recordings from single neurons enable dissection of the brain activities that underlie mental operations. The new works illustrate that neurons in the frontal region of the brain (or neuronal ensembles, or brain areas) may dynamically and adaptively switch between multiple functions. During a dynamic decision-making task is involved the comparison of two quantities (two frequencies of vibration presented to a fingertip), separated by a delay [2].
Such techniques as functional magnetic resonance imaging (fMRI) and electrical recordings from single neurons enable dissection of the brain activities that underlie mental operations. The new works illustrate that neurons in the frontal region of the brain (or neuronal ensembles, or brain areas) may dynamically and adaptively switch between multiple functions. During a dynamic decision-making task is involved the comparison of two quantities (two frequencies of vibration presented to a fingertip), separated by a delay [2].
The mental operations involved in this quantity-comparison task in frontal region included:
- Perceiving the first signal S1, holding in working memory for several seconds,
- Perceiving the second signal S2, and
- Deciding whether it was of lower or higher quantity than the first.
Neurons in the secondary somatosensory cortex of monkey brain remained silent in the delay interval between S1 and S2, their preferences remained invariant. Neurons in the prefrontal cortex, by contrast, showed differential preferences for the low versus high quantity also during the delay interval, during which they sustained their preferential firing patterns. In the decision phase, however, prefrontal cortex neurons no longer encoded information about high versus low quantities, but rather encoded information for "S2 < S1 " or "S2 > S1", respectively.
The firing rates of single neurons in the prefrontal cortex:
- First encode the quantity of S1,
- Then represent the active maintenance of that quantity in working memory, and
- Finally reverse sign to encode the appropriate decision.
Machens., et al. results clearly show that the networks of prefrontal cortex neurons can dynamically adapt and reconfigure the encoding functions represented in their firing patterns as the cognitive flow develops, without changing their connectivity [3].
Neurons know when to encode a particular activity:
- Cognitive control should be envisioned as emergent properties of the neural network configuration,
- More elementary mechanistic processes being tailored to allow new functions to emerge.
Probabilistic coding applies:
- Within-trial changes in the firing patterns of prefrontal cortex neurons,
- The emergence of cognitive control through learning,
- The specialized higher order nature of process called performance-error monitoring
- A new function that emerges,
- From more basic neural mechanisms for conflict detection,
- Which usually reside in medial frontal cortex (MFC) neurones,
- Detecting the simultaneous activation of competing correct and incorrect responses.
Both error detection and conflict monitoring are part of the computational process in which activation of MFC neurons is proportional to the perceived likelihood of an error taking place [4,5]. The representations of the likelihood of error by the MFC develop through experience. Such representations build:
- On reinforcement-learning processes,
- Mediated by phasic decreases in midbrain dopamine projections to the MFC when ongoing events turn out worse than expected.
The MFC as Global Workspace (GW) determines:
- Which goals may not be achieved,
- A rewards may not be obtained unless the level of cognitive control is subsequently increased.
This increase in cognitive control takes place:
- When a response conflict indicates a reduced probability of obtaining a reward,
- When errors signal the loss of an anticipated reward,
- The context predicts the likelihood of imminent errors.
These patterns of neural firing confirm that the principal task of the MFC-GW is:
- To monitor performance,
- To compute and signal the likelihood of obtaining or losing rewards in response to particular actions [13],
- Guides decisions about which actions are worth taking [6].
The probabilistic error-likelihood model of the GW in consciousness must incorporate a transient disengagements of MFC activity that predict errors. Occasional lapses and other forms of variability are characteristics of all cognitive processes [17]:
- The fMRI revealed greater activity in the MFC during the high-error change trials compared with low-error change trials,
- MFC activity increased with practice, reflecting an improved ability to predict the likelihood of making an error.
The toponeural structure (TNS) can itself be divided into a subsystem that is open to energy and information flow, and the subsystem´s environment: larger dual topological complex (L-DTC). The whole combined system still obeys the second law of thermodynamics, but it is possible that the subsystem: smaller dual topological complex (S-DTC) can experience a decrease of entropy at the expense of environment [16].
The entropy increase in the “sub-system environment” is guarantied by the second law, to more than offset the entropy decrease in the smaller, but main dual topological complex (M-DTC). The subsystem can only be maintained away from equilibrium as long as there is usable energy in environment. When the environmental energy at maximum (no usable energy), the subsystem is guaranteed itself proceed to equilibrium [21].
Toponeuronal model of the MFC
The medial frontal cortex (MFC) is a comparator system, which is the basis of global workspace (GW) in the human brain. As it proposes B. Baars [8,9], the consciousness is the result of a GW and distributes information to the huge number of parallel modules-processors that form the rest of the brain. The GW can be seen as main dual toponeuronal complex (M-DTC), correlated through GM with other modules: smaller DTCs (S-DTCs). The large complex of GW is formed by M-DTC plus S-DTCs.
The medial frontal cortex (MFC) is a comparator system, which is the basis of global workspace (GW) in the human brain. As it proposes B. Baars [8,9], the consciousness is the result of a GW and distributes information to the huge number of parallel modules-processors that form the rest of the brain. The GW can be seen as main dual toponeuronal complex (M-DTC), correlated through GM with other modules: smaller DTCs (S-DTCs). The large complex of GW is formed by M-DTC plus S-DTCs.
Self-similarity between contents of the GW, endomorphisms (E) (internal transformation reshaping itself) and their shapes is mapped (simulated, replicated) into working memory (WM), if lead to the Morita-I, II, III, equivalence, could form the Self (consciousness) online circuit. Conscious are all contents of GW which are in real time restriction mapping an online reentry to WM. Consciousness can be under stand as a neural online simulation generated in the frontal cortex of the brain. The stimulus beyond the GW is unconscious.
Based upon the reciprocal connections of the cingulated cortex with the hypothalamus, Paper proposed that the cingulated cortex is involved in the subjective experience of emotions (EQ). Now it is suggested the anterior cingulated cortex (ACC) is involved in detecting when strategic control is required and the lateral prefrontal cortex is involved in strategic control. Some current findings are supporting the role of the ACC as an autonomic regulator during a need to monitor the sympathetic system. During cognitive activity, ACC activity begins within the first 150ms of a task that takes ~ 1100 ms. Although the heart rate does speed up during target processing, it also tends to slow down while waiting for targets [25].
It has been proposed that the ACC plays a prominent role in the executive control of cognition, and could also participate in processing information and subjective faithful states. We propose that implementing a comparator process, the ACC monitors competition between processes that conflict during task performance. Dipole modeling suggests that an error-related negativity (ERN) has a medial frontal generator, possibly the ACC. The role of ACC in higher level cognition include the hypothesis that it is involved with late selection as attention to action, and is also responsive to errors, and may by a candidate for main dual toponeuronal complex (M-DTC) [26].
The alternative leads to the idea of immediate interaction of y-function of macro-state (let's name it w-function) with y-function of micro-state. The notion of w-function has the content only when this w-function is marked in the macro-world. Otherwise w º y. Therefore, by calculating statistical weight of such a state (its logarithm due to Boltzmann equation is equal to the entropy with the accuracy up to a constant) we must not sum up the probabilities of alternative microstates, but multiply conditional probabilities of all succession microstates, composing the "thickness" of present for the given living macrostate [21].
This multiplication results in the statistical weight value less than one and, hence, to the negative value of entropy. Such re-normalization is a constant outer interference (topological neighborhood function), namely, from macro-state side having its own plot, image into the natural dynamics of microstates. And in this case the element of "miracle", i.e., discrepancy of the observed processes at the micro level for the second law of thermodynamics, and uncertainty of future to past, is introduced into the natural dynamics. The measure of this element is anti-entropy [22], and w-y-interaction (re-normalization of probabilities) is the mechanism of anti-entropy origination. We note that most theories of conscious processing have failed to recognize the important role of spontaneous thalamocortical activity within a distinct set of GW neurons [24].
Self
Topology of the Self
Topographic means that a sensory receptor sheet receiving signals from the world connects to its recipient map in such a way that neighboring locations in the sensory sheet are also neighboring locations in the recipient map. The interaction of multiple restriction maps can be coordinated in the same way. Coupling the outputs of multiple maps reentrantly connected to the sensorymotor behavior is achieved through a higher-order structure of global restriction mapping (GM). GM is a dynamic structure containing multiple reentrant local maps (motor and sensory) able to interact with non-mapped parts of the brain (the hippocampus, the basal ganglia and the cerebellum).
Topology of the Self
Topographic means that a sensory receptor sheet receiving signals from the world connects to its recipient map in such a way that neighboring locations in the sensory sheet are also neighboring locations in the recipient map. The interaction of multiple restriction maps can be coordinated in the same way. Coupling the outputs of multiple maps reentrantly connected to the sensorymotor behavior is achieved through a higher-order structure of global restriction mapping (GM). GM is a dynamic structure containing multiple reentrant local maps (motor and sensory) able to interact with non-mapped parts of the brain (the hippocampus, the basal ganglia and the cerebellum).
The brain carries out a process of conceptual “self-categorization”, by matching past perceptual categories with signals from value systems, carried out by cortical systems capable of conceptual functions. Perceptual experience arises from the correlation by a conceptual memory of a set of ongoing perceptual categorizations [15].
Self (the social selfhood) Internal systems arise from interactions between the limbic and the cortical systems (brain stem, hypothalamus, autonomic centers).
Nonself (other entities) Differing from the Self the outside-world systems are strictly cortical (primary and secondary cortex for sight, hearing, touch, etc.) Both have correlations (through reentrant mapping) in hippocampus, amygdala, septum, and special value-category memory in frontal, temporal and parietal cortex.
Suppose that the Self can be defined as a set S with only one member: S itself. S is introduced as a quality in order to have a variable. Now suppose there is a topological space X in which this information is distributed. We will define a group of spatially distributed sensations as subset A disjointed from the complement subset non A. Accordingly, the intersection of A and non A will form an empty set: A and non A = 0. Depending on which information S is focused on it will also be embedded in the respective and in turn distinct subspace or it will be split into two disjointed subsets S1 or S2.
This correlation encoding the entire structure perceived by the Self is a scale-invariant magnification of each part of it. A solution for equation with x = S and X is then given by the power law: f (x) = C x (1-D) Where, C is a constant and D = lim (x to 0) [log N(x)/log (1/x)].
The tiling of the world in our mind
The primary goal is to develop a figurative but still completely abstract algorithm for the realization of spatial information perceived in our consciousness. The smallest fractal d {SX} could representing the elementary tile for the construction of space perceived in consciousness. The metric underlying the elementary tile d {SX} can be formed by a coordinate system with the principle axes xi lying in the plane enclosed by the tile.
The primary goal is to develop a figurative but still completely abstract algorithm for the realization of spatial information perceived in our consciousness. The smallest fractal d {SX} could representing the elementary tile for the construction of space perceived in consciousness. The metric underlying the elementary tile d {SX} can be formed by a coordinate system with the principle axes xi lying in the plane enclosed by the tile.
In order to describe the perception of space by an inner observer it is suggested that these vectors generate the three components Xi, Yi, Zi for one point in a three-dimensional space perceived by the Self. The respective operation "lifts up" the spatial information given by the fractal in R2 to a point seen in R3. The eye representing the Self, as the inner observer of visual information, adopts a dual position in either R2 or R3, indicating a general consideration for any RN. The components of any point perceived in consciousness are subject to transformation to a coordinate system opposite to the position of the observer [7].
Each elementary tile behaves like a "point", but forms a connected space with other tiles covering the entire coherent lattice. The size of adjacent fractals may vary depending on the actual coherence length. This does not violate the principle of self-similarity, but gives rise to points in R3 with different distance to R2 and may distribute them in a three-dimensional space as it is experienced in our mind. It should be emphasized that the space perceived in consciousness is not to be assigned to Euclidean space, but to Grothendieck topology in the brain.
Suppose that in a pre-coherent state t< tc the Self S hits the space intervals dx1 = xc-x1 and dx2 = x2-xc with the probabilities p1 (dx1) and p2 (dx2). The distribution of the Self is then given by a Markov operation according to fractal image construction:
M (v) = p1 v(S) w-1(dx1) + p2 v(S) w-1(dx2)
With w (dx) = Hutchinson operator with w-1 = pre-image on dx
V (S) = integral of {u (dx, t) dx}
U (dx, t) = distribution density of "S" on the pre-image.
M (v) = p1 v(S) w-1(dx1) + p2 v(S) w-1(dx2)
With w (dx) = Hutchinson operator with w-1 = pre-image on dx
V (S) = integral of {u (dx, t) dx}
U (dx, t) = distribution density of "S" on the pre-image.
An iteration of w (dx) leads to a fractal distribution of S on sequentially contracting intervals of dx. After sufficient downscaling iterations, S is driven to the attractor xc+/-dxl which is equivalent to the point of coherence. The probabilities for the distribution of S onto dx derived from the Markov process are transformed into those for the description of a coherence equilibrium. An autonomous organism must be capable of generating spontaneous representations and intentions (Self-activation). The [24] shows how spontaneous membrane oscillations and noisy synaptic transmission can be harnessed to generate a stream of highly organized states of Self-activation. This may play a role in the spontaneous generation of novel, flexible behavior. The strongly recurrent connectivity of cortical neurons in association areas collectively form a conscious workspace, an internal space buffered from outside world and within which mental hypotheses can be entertained and discarded at will.
Mathematical Intuition
The neural basis of the logarithmic mental number line
In the early days of neurophysiology, a few neurons that encoded number were reported in the association cortex. Nieder and Miller [10] recorded in monkey prefrontal cortex the number neurons (Principal sulcus, Arcuate sulcus). It was recording also in parietal cortex, and also in prefrontal cortex, reported the observation of neurons whose firing rate was tuned to a specific numerosity. This was possible to examine the neural code for an abstract psychological continuum. There is often evidence that the stimulus compression occurs at a peripheral sensory level. Information is classically defined as reduction of the uncertainty, measured by the entropy function [16], which is the weighted sum of the logarithm of probability (p) of alternatives outcomes (i): - Σ pi log2 pi. The neural code for number can be also described in better way by logarithmic than by a linear scale. The monkeys encode the numerosities on an approximate compressed scale confirms that this approximation is the natural way that number is encoded in a brain without language [11,12].
The neural basis of the logarithmic mental number line
In the early days of neurophysiology, a few neurons that encoded number were reported in the association cortex. Nieder and Miller [10] recorded in monkey prefrontal cortex the number neurons (Principal sulcus, Arcuate sulcus). It was recording also in parietal cortex, and also in prefrontal cortex, reported the observation of neurons whose firing rate was tuned to a specific numerosity. This was possible to examine the neural code for an abstract psychological continuum. There is often evidence that the stimulus compression occurs at a peripheral sensory level. Information is classically defined as reduction of the uncertainty, measured by the entropy function [16], which is the weighted sum of the logarithm of probability (p) of alternatives outcomes (i): - Σ pi log2 pi. The neural code for number can be also described in better way by logarithmic than by a linear scale. The monkeys encode the numerosities on an approximate compressed scale confirms that this approximation is the natural way that number is encoded in a brain without language [11,12].
Neural coding of expected value (EV)
Comparative theorists proposed that regions innervated by mesolimbic dopamine projections play a critical role in the computation of EV. Because fMRI studies also indicate that:
Comparative theorists proposed that regions innervated by mesolimbic dopamine projections play a critical role in the computation of EV. Because fMRI studies also indicate that:
- Gain outcomes instead activate the mesial prefrontal cortex (MPFC),
- The outcomes involve a collapse of probability,
- Increased gain probability (PRB) might increase MPFC activation, even during anticipation,
- The ventral tegmental area midbrain dopamine neurons that project to the nucleus accumbens (NACC), and MPFC have also been implicated in the computation of EV.
The main effect of probability coding is correlated:
- With activation foci in the bilateral MPFC,
- The left parahipocampal gyrus,
- The posterior cingulate.
The interaction MAG (gain magnitude) by PRB was only correlated with activation foci in the bilateral medial caudate and right putamen.
The bilateral MPFC showed activity consistent with representation of:
- The probability,
- The value terms of EV.
The bilateral anterior cingulate activation might relate to integration of these two terms:
- The value and probability terms of EV.
Investigation of the neural correlates of EV, mesolimbic regions (including the midbrain, NACC, and MPFC) showed activation correlated with a linear model of EV. Whereas NACC activity correlated only with anticipated MAG, MPFC activity also correlated with anticipated gain probability.
MPFC activation was associated with the perceived probability of obtaining large gains. These findings suggests, that distinct mesolimbic regions play different roles in EV computation. The MPFC showed linear but not quadratic trends, supporting probabilistic rather than uncertainty-based interpretations.
Intuition probability at microscopic level
Probabilities of the mathematical intuition (MI) at the microscopic level are governed by interfering probability amplitudes rather than by additive probabilities. In accordance with the Bohr´s correspondence principle the quantum scalar product wm,n between two stationary states um and vn can be visualized as the overlap between two states depicted in x - p oscillator phase space as occupied bands traversed in a clockwise direction. The total probability amplitude wm,n is the sum of contributions A1/2 m,n exp (± i φm,n) from the two zones. Here the phase φm,n is area between the center lines of the two states. The area-of-overlap concept illustrates the interference in phase space [23].
Probabilities of the mathematical intuition (MI) at the microscopic level are governed by interfering probability amplitudes rather than by additive probabilities. In accordance with the Bohr´s correspondence principle the quantum scalar product wm,n between two stationary states um and vn can be visualized as the overlap between two states depicted in x - p oscillator phase space as occupied bands traversed in a clockwise direction. The total probability amplitude wm,n is the sum of contributions A1/2 m,n exp (± i φm,n) from the two zones. Here the phase φm,n is area between the center lines of the two states. The area-of-overlap concept illustrates the interference in phase space [23].
Interfering areas of overlap in phase space as a measure of interfering transition probability amplitudes brings us to Wigner´s phase
space function, which provides directly the probability . The overlap between the Wigner functions Pm(W) and Pn(W) when
integrated over the total phase space, yields the probability Wm,n:
The Wigner function approach deals in terms of probabilities [19]. Interference effects must therefore originate from phase space domains where the Wigner function product Pm(w). Pn(w) Assumes also negative values. The jump probability Wm,n is the weighted overlap in phase space between the Wigner functions representing the two quantum states. The main effect of probability is negatively correlated: with activation foci in the left anterior cingulate, left insula, bilateral medial caudate, right putamen. Mathematical intuition (MI) is based on the inputs from number neurons, without Morita equivalence in circuit, mapped to the mesial prefrontal cortex (MPFC) in a process computed due the complex probability amplitudes. Intuition (I) than means mapping of number neurons to the nucleus accumbens (NACC), based on computations of added probability.
Conclusions
Despite widespread acceptance of the idea that perception involves inference, probabilistic models of inferences have only recently entered mainstream neuroscience and psychology. David Marr described the output of the system as a function of its input [14]. To make distinguishability clear, we should use linear probabilities (intuition-I), or the complex probability amplitudes (mathematical intuition-MI). The last represents not linearly related quantities that lie on a sector of a plane, but quadratically related quantities that lie on a sector of a sphere. But medial frontal cortex (MFC) functioning as global workspace (GW), and Self as a toponeuronal structure (TNS), are also a product of probabilistic coding in neurones.
Dehaene [11] suggest that the exact arithmetic puts emphasis on language-specific representations based on a left inferior frontal circuit, and is also used for generating associations between words. Symbolic arithmetic is seen as a cultural invention specific to humans, and depended on the improvement of number computing systems. The other domains of mathematics, as calculus, may depend critically on the invention of an appropriate mathematical language. Simple calculations activate a distributed network involving the parietal, prefrontal and premotor cortices. The posterior parietal cortex and prefrontal cortex are functionally interconnected, information could be transferred to the prefrontal cortex, where amplified, may be able to gain control over behavior.
We predict that at the biological (neuronal) level a complex phenomena as for instance the neuroplasticity is, will be not fully understandable due this physically defined term of information. The biological level needs a more stochastic, probabilistic definition of information. The coming definition must reflect that every new information as innovation, is changing the values of probabilities of the system, at least due microscopic changes in its correlations in a given topological space, or domain. These changes in probabilities are encoded due the global restriction mapping based on neuronal group selection. Information at the biological level must be defined through a more flexible, more “live” flow, than it is obviously done with Shannon-type definitions working at the level of physics. Also Prigogine [20] pointed that the existence of phase transitions shows we have to be careful when we adopt a reductionist attitude. This flexible, live flow can be approached by the variable topology, and Riemannian manifold.
By Gödel [18], predictions are like a perception of the objects of set theory. Prediction is a mode of MI, which in sense of perception induces building up theories of the future. The given underlying mathematics is closely related to the abstract elements contained in our empirical ideas. The brain seems to have internal theories about what the world is like. Between brain theories is internal perceptual rivalry in Darwinian sense. The world as a system can be described due the polar decomposition, as a whole system consisting from two subsystems (Self subset A, and Non-self-subset non A), mutually observing one another.
References
- Christopher D Fiorillo., et al. Discrete Coding of Reward Probability and Uncertainty by Dopamine Neurons”. Science 299. 5614 (2003): 1898-1902.
- KR Riderinkhof., et al. “Adaptive Coding”. Science 307.5712 (2005): 1059-1060.
- CK Machens., et al. “Flexible Control of Mutual Inhibition: A Neural Model of Two-Interval Discrimination”. Science 307.5712(2005): 1121-1124.
- JW Brown and TS Braver. “Learned Predictions of Error Likelihood in the Anterior Cingulate Cortex”. Science 307.5712 (2005): 1118-1121.
- B. Knutson., et al. “Distributed Neural Representation of Expected Value”. The Journal of Neuroscience 25.19(2005): 4806-4812
- W. Schulz. “Neural coding of basic reward terms of animal learning theory, game theory, microeconomics and behavioural ecology”. Current Opinion in Neurobiology 14.2 (2004): 139-147.
- E Bieberich. “Structure in human consciousness: A fractal approach to the topology of the self-perceiving an outer world in an inner space”. Medical College of Virginia Campus of Virginia Commonwealth University, Richmond, VA, (2002)
- B Baars. “In the theatre of consciousness. Journal of Consciousness Studies 4 (1997): 292-309.
- B. Baars. “Cognitive Theory of Consciousness”. Cambridge U. P., New York (1988).
- A Nieder., et al. “Representation of the quantity of visual items in the primate prefrontal Cortex”. Science 297.5587 (2002): 1708-1711.
- S Dehaene., et al. “Sources of mathematical thinking: behavioral and brain-imaging evidence”. Science 284.5416 (1999): 970-974.
- S Dehaene. “The neural basis of the Weber-Fechner Law: a logarithmic mental number line”. Trends in Cognitive Sciences 7.4 (2003): 145-147.
- S Dehaene., et al. “A neuronal model of a global workspace in effortful cognitive tasks”. Proceedings of the National Academy of Sciences of the United States of America 95.24 (1998): 14529-14534.
- J McDermott. “Brain models: the next generation”. Nature Neuroscience 5.9 (2002).
- G Tononi and G Edelman. “Consciousness and Complexity”. Science 282.5395 (1998): 1846-1851.
- G Tononi. “An information integration theory of consciousness”. BMC Neuroscience 5 (2004): 42.
- M Raichle. “The neural correlates of consciousness: an analysis of cognitive skill learning”. Philosophical Transactions of the Royal Society B: Biological Sciences 353.1377 (1998): 1889-1901.
- K Gödel. “What Is Cantor´s Continuum Problem?” The American Mathematical Monthly 54.9 (1947): 515-525.
- E Wigner. “Quantum Optics, Experimental Gravitation, and the Measurement Theory”. P. Meystre, N. Scully, eds., Plenum, New York (1983).
- I Prigogine. The End of Certainty. Time, Chaos and the New Laws of Nature. New York, The Free Press (1997).
- G Mikhailovsky. “Biological Time, its Organization, Hierarchy and Representation by Complex Values”. EReports, Moscow (2000).
- N Kobozev. “Investigations in the Field of Thermodynamics and Thinking Processes”. Moscow (in Russian) (1971).
- J Wheeler., et al. “Interference in Phase Space”. Annalen Der Physik 48.7 (1991): 423-502.
- S Dehaene and JP Changeux, “Ongoing Spontaneous Activity Controls Access to Consiousness: A Neuronal Model for Inattentional Blindness”. PLOS Biology 3.5 (2005).
- Luu P and Posner MI. “Anterior cingulate cortex regulation of sympathetic activity”. Brain 126 (2003): 2119-2020.
- Carter CS., et al. “Anterior Cingulate Cortex, Error Detection, and the Online Monitoring of Performance”. Science 280.5364 (1998): 747-749.
Citation:
Robert Skopec. “Global Workspace, Self, and Mathematical Intuition”. Current Opinions in Neurological Science 2.5 (2018):
532-540.
Copyright: © 2018 Robert Skopec. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.






























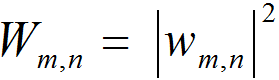
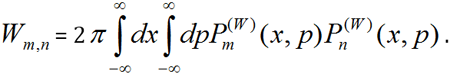
 Scientia Ricerca is licensed and content of this site is available under a Creative Commons Attribution 4.0 International License.
Scientia Ricerca is licensed and content of this site is available under a Creative Commons Attribution 4.0 International License.