Research Article
Volume 1 Issue 3 - 2017
A Detailed Study of Transition Metal Complexes of a Schiff Base with Its Physico-Chemical Properties by Using a Electrochemistry Method
Netaji Subhas Chandra Bose Institute of Pharmacy, West Bengal, India
*Corresponding Author: Anindya Bagchi, Assistant Professor Netaji Subhas Chandra Bose Institute of Pharmacy, West Bengal, India.
Received: May 19, 2017; Published: July 05, 2017
Abstract
Activities of metal ions in biology have stimulated the development of metal based therapeutics. It has been found that biologically active compounds became more effective and bacteriostatic upon chelation with metal ions. The present work deals with the synthesis of metal (Cu and Zn) complexes derived from a novel Schiff base drug synthesized from urea and salicylaldehyde and its physico-chemical analysis was carried out to find out ligand- metal ratio of this complex in solution. For the determination of complexing nature of these complexes “Monovariation method (Mole ratio method/Yoe-Jones Method)” have been used to ascertain the ligand-metal ratio in the complex. The stability constant of the formed complexes was calculated by molar conductance measurement using Modified Job’s method (Method of Continuous Variations). The analysis was been carried out by using conductometry. To confirm metal-ligand ratio, conductometric titrations was been carried out at room temperature using analytical grade metal salts. Titrations were carried out with “systronics conductivity-meter” using dip type conductivity cell having cell constant 1 at room temperature. Data after the analysis showed the formation of 1:1 [M: L] ratio in the case of Cu ion and 1:3 [M:L] in the case Zn ion. The coordination behavior of the metal ions towards to the investigated Schiff base takes place through –C=N and –OH groups.
Keywords: Yoe-Jones Method; Conductometry; Modified Job’s method; Chelation; Metal ions
Introduction
Long before the chemist S. M. Jorgensen (1837-1914) started his extensive studies on the synthesis of complex compounds in which metal halides and other salts could give compounds with neutral molecules it was known that many of these compounds could easily be formed in aqueous solutions. The recognition of the true nature of complexes originated with Alfred Werner (1866-1914), followed by the ideas of G. N. Lewis and N. V. Sidgwick, who proposed that the chemical bond requires the sharing of an electron pair. This led to the concept that a neutral molecule with an electron donor, Lewis base can donate these electrons to a metal ion or an electron acceptor Lewis acid.
The d-block elements are elements which have partly filled d- shell in many of their commonly occurring oxidation states such as copper, zinc etc. They are all hard, with high melting and boiling points. They conduct heat and electricity well, form alloys with one another and with other metallic elements. Many of them are highly electropositive to dissolve in mineral acids, although a few are noble i.e. have low electrode potentials and hence are unaffected by simple acids. Many of them exhibit variable valency, and their ions and compounds are coloured [1]. The intense colour of metal chelates is due to charge transfer transitions. This is simply the movement of electrons from the metal ion to the ligand or vice versa. Such transitions include promotion of electrons from levels in the ligand or from a σ bonding orbital to the unoccupied orbital of the metal ion or promotion of σ- bonded electrons to unoccupied orbital of the ligand [2].
The Schiff base ligands and their metal complexes have specific importance in the field of coordination chemistry. As the present work deals with the complexes of Schiff base ligands, it is mandatory to include a brief general discussion on the chemistry of Schiff bases and their metal complexes. Hugo Schiff, a German chemist, isolated [3] the first condensed product of amines with carbonyl compounds, which was referred as Schiff base as the compounds containing an Azomethine group (-CH=N-).
Where “R” may be an aliphatic or aromatic group. Schiff’s bases of aliphatic aldehydes are relatively unstable and are readily polymerizable [4-6]. While those of aromatic aldehyde having an effective conjugation system are relatively more stable [7-10]. Schiff bases are generally bi or tri-dentate ligands capable of forming very stable complexes with many transition metals. In Medicinal chemistry Schiff’s base has versatile medicinal use [11-13].
Previously a considerable interest has been focused on the complexing property of bi, tri and tetradentate Schiff base ligands having oxygen-nitrogen, oxygen-sulphur, nitrogen-sulphur and oxygen-nitrogen-sulphur as potential donor sites [14]. The Schiff bases are considered as useful chelating agents when a suitable functional groups like –OH, -SH, or -NO2 etc. are present sufficiently close to the azomethine group so as to form five or six membered chelating ring upon reaction with the metal ion. Most of the cases for the stability of the complexes have centred on the ligand properties and not on those of the metal ion [15].
Such a Schiff base and its complexes has been synthesized and used in the present work which is made from urea and salicylaldehyde:
Material and Methods
Monovariation method (Mole ratio method/Yoe-Jones method)
This method was introduced by Yoe and Jones [16]. Number of solutions were prepared in which the total concentration of the metal is kept constant and the concentration of the ligand is varied under similar condition. A plot is prepared by conductance as a function of the ratio of moles of ligand against the moles of the metal. This plot expected to give straight line from the origin to the point where equivalent amounts of the constituents are present; the curve will then become horizontal if only one complex of high stability is formed. The corresponding point at the molar ratio axis to each intersecting point gives directly the ligand to metal ion ratio in each complex.
This method was introduced by Yoe and Jones [16]. Number of solutions were prepared in which the total concentration of the metal is kept constant and the concentration of the ligand is varied under similar condition. A plot is prepared by conductance as a function of the ratio of moles of ligand against the moles of the metal. This plot expected to give straight line from the origin to the point where equivalent amounts of the constituents are present; the curve will then become horizontal if only one complex of high stability is formed. The corresponding point at the molar ratio axis to each intersecting point gives directly the ligand to metal ion ratio in each complex.
Modified Job’s method (Method of Continuous Variations)
The modification of the Job's [17] continuous variation method performed by Vesburge and Cooper [18] was applied to find the stoichiometric and formation constant of the complex. The case of co-ordination may be described by:
mM + nL = MmLn
The modification of the Job's [17] continuous variation method performed by Vesburge and Cooper [18] was applied to find the stoichiometric and formation constant of the complex. The case of co-ordination may be described by:
mM + nL = MmLn
A series of solutions are prepared in which the sum of total concentration of M and L is kept constant but their proportions are continuously varied. The conductance of the series is plotted against the mole fraction of the ligand. The ratio of the stoichiometric coefficients is determined from the mole fraction at the point of intersection formed by extrapolation of the two sides of the triangle.
Conductometric titration [19]
The electrical current through a chemical cell is carried out by the ionic species in the solution conductometrically. The ease with which current is conducted through a solution (under the influence of potential difference applied across two electrodes) is mainly depends upon the concentrations and kind of ions in the solution. If two suitable electrodes are present in a solution and potential difference is applied across those electrodes then current will flow through the solution. During progress of a conductometric titration changes in the conductivity of the solution usually occur and at the end point involving neutralization or precipitation reaction the conductivity of the solution will be minimum. The equivalence point may be located graphically by plotting the change in conductance as a function of the volume of titrant added. The present account details deals with the synthesis of metal complexes (Cu & Zn) derived from a Schiff base drug synthesized from urea and salicylaldehyde and their physico-chemical analysis was carried out to find out ligand- metal ratio of these complexes in solution by using conductometric method.
The electrical current through a chemical cell is carried out by the ionic species in the solution conductometrically. The ease with which current is conducted through a solution (under the influence of potential difference applied across two electrodes) is mainly depends upon the concentrations and kind of ions in the solution. If two suitable electrodes are present in a solution and potential difference is applied across those electrodes then current will flow through the solution. During progress of a conductometric titration changes in the conductivity of the solution usually occur and at the end point involving neutralization or precipitation reaction the conductivity of the solution will be minimum. The equivalence point may be located graphically by plotting the change in conductance as a function of the volume of titrant added. The present account details deals with the synthesis of metal complexes (Cu & Zn) derived from a Schiff base drug synthesized from urea and salicylaldehyde and their physico-chemical analysis was carried out to find out ligand- metal ratio of these complexes in solution by using conductometric method.
Calibration of conductivity meter
A Systronics model 306 Conductivity Meter with Conductivity Cell and a simple weight machine from Eagle and a Borosilicatate Glass was used. Conductance reading was noted which having the unit called Siemens.
A Systronics model 306 Conductivity Meter with Conductivity Cell and a simple weight machine from Eagle and a Borosilicatate Glass was used. Conductance reading was noted which having the unit called Siemens.
Synthesis of Schiff Base compound
Urea (SRL, India 1 gm, 0.02M) was dissolved in 1ml of double distilled water and cooled to 0ºC in ice bath. Salicylaldehyde (Merck, India, 1.2 gm, 0.01M) was taken separately in 1ml alcohol and cooled to 0ºC. After that Salicylaldehyde was added to urea solution in 100 ml conical flask slowly with stirring at room temperature. The solution was again stirred for half an hour at room temperature (20ºC) in a magnetic stirrer with the addition of 4 drops of NaOH (10%), and then allowed to stand for half an hour. Soon after that 2 ml water-alcohol (1:1) was added to the reaction mixture and was place in ice bath for one hour. Yellow precipitate obtained after addition of sufficient amount of 10% NaOH and was filtered, washed in cold alcohol and re-crystallized in alcohol. The compound (yield 68%) was dried over vacuum. The structure of the compound has been determined by UV, IR MASS and NMR spectrophotometric studies which has been previously established [20]. The proposed chemical name of this compound is Bis-(2-hydroxy-N-benzyl) Urate.
Urea (SRL, India 1 gm, 0.02M) was dissolved in 1ml of double distilled water and cooled to 0ºC in ice bath. Salicylaldehyde (Merck, India, 1.2 gm, 0.01M) was taken separately in 1ml alcohol and cooled to 0ºC. After that Salicylaldehyde was added to urea solution in 100 ml conical flask slowly with stirring at room temperature. The solution was again stirred for half an hour at room temperature (20ºC) in a magnetic stirrer with the addition of 4 drops of NaOH (10%), and then allowed to stand for half an hour. Soon after that 2 ml water-alcohol (1:1) was added to the reaction mixture and was place in ice bath for one hour. Yellow precipitate obtained after addition of sufficient amount of 10% NaOH and was filtered, washed in cold alcohol and re-crystallized in alcohol. The compound (yield 68%) was dried over vacuum. The structure of the compound has been determined by UV, IR MASS and NMR spectrophotometric studies which has been previously established [20]. The proposed chemical name of this compound is Bis-(2-hydroxy-N-benzyl) Urate.

Salicylaldehyde Urea Bis-(2-hydroxy-N-benzyl) Urate
Figure 2: Estimated structure of Bis-(2-hydroxy-N-benzyl) Urate.
Figure 2: Estimated structure of Bis-(2-hydroxy-N-benzyl) Urate.
Preparation of chelates
The chelates under investigation were prepared by mixing 30 ml ethanolic solution of the Schiff base (2.68g; 0.01 mol) with the same amount of ethanolic solution of the metal salts (0.01 mol); Cu-acetate (1.99g), Zn- acetate (2.19g). If the chelates did not isolate, few drops of ammonium hydroxide were added to adjust the pH = 8. The reaction mixture was refluxed with stirring for 3h and then filtered, collected. The chelates were dried in desiccators over anhydrous CaCl2 under vacuum. (Yield: Cu-acetate: 75%, Zn-acetate: 76%).
The chelates under investigation were prepared by mixing 30 ml ethanolic solution of the Schiff base (2.68g; 0.01 mol) with the same amount of ethanolic solution of the metal salts (0.01 mol); Cu-acetate (1.99g), Zn- acetate (2.19g). If the chelates did not isolate, few drops of ammonium hydroxide were added to adjust the pH = 8. The reaction mixture was refluxed with stirring for 3h and then filtered, collected. The chelates were dried in desiccators over anhydrous CaCl2 under vacuum. (Yield: Cu-acetate: 75%, Zn-acetate: 76%).

Proposed Structure of Schiff’s base metal complex (M=Zn)
Figure 3: Proposed Structures of Schiff’s Base Chelate.
Figure 3: Proposed Structures of Schiff’s Base Chelate.
Conductometric titrations for detection of Metal-Ligand ratio (Monovariant method) [21]
Solution of drug (Schiff’s Base) having strength 0.01M was prepared with water in 100 ml. Similarly, 0.01 M of metal salts (Cupric acetate and Zinc acetate) was prepared and suitably diluted as and when required. Ligand solution was taken in a beaker and this was titrated conductometrically against 0.01M metal salt solution taken in a burette. Conductance was recorded after every addition of 0.5 ml of metal salt solution with constant stirring at constant temperature. Volume corrections were applied as:
Conductance = {(V+v)/V}*(Observed Conductance)
Where, V = initial volume of ligand solution, v = volume of metal solution added.
The correction presupposes that the conductivity is a linear function of dilution. Results were plotted in the form of a graph between corrected conductance and volume of metal salts.
Solution of drug (Schiff’s Base) having strength 0.01M was prepared with water in 100 ml. Similarly, 0.01 M of metal salts (Cupric acetate and Zinc acetate) was prepared and suitably diluted as and when required. Ligand solution was taken in a beaker and this was titrated conductometrically against 0.01M metal salt solution taken in a burette. Conductance was recorded after every addition of 0.5 ml of metal salt solution with constant stirring at constant temperature. Volume corrections were applied as:
Conductance = {(V+v)/V}*(Observed Conductance)
Where, V = initial volume of ligand solution, v = volume of metal solution added.
The correction presupposes that the conductivity is a linear function of dilution. Results were plotted in the form of a graph between corrected conductance and volume of metal salts.
Modified Job’s Method of continuous variation [22] for determining composition and stability constant of complex
Equimolar solutions of ligand and metal solutions were prepared and three series C1, C2, C3 of solutions were made. In set C1 metal salt solution was filled with volume 0.0ml to 12.0 ml and total volume was made to 12.0 ml in each. Similarly, in C2 ligand solution was filled and set C3 was prepared by mixing metal salt solution from 0.0ml to 12.0 ml and ligand solution from 12.0 ml to 0.0 ml. Conductance was recorded for each solution. Δ Conductance was calculated as “C1+C2-C3” [23]. Graphs was plotted between corrected conductance and mole metal-ligand ratio. The composition and stability constants were determined from the equivalence point in the graph [24].
Equimolar solutions of ligand and metal solutions were prepared and three series C1, C2, C3 of solutions were made. In set C1 metal salt solution was filled with volume 0.0ml to 12.0 ml and total volume was made to 12.0 ml in each. Similarly, in C2 ligand solution was filled and set C3 was prepared by mixing metal salt solution from 0.0ml to 12.0 ml and ligand solution from 12.0 ml to 0.0 ml. Conductance was recorded for each solution. Δ Conductance was calculated as “C1+C2-C3” [23]. Graphs was plotted between corrected conductance and mole metal-ligand ratio. The composition and stability constants were determined from the equivalence point in the graph [24].
In the present work the study was carried out using Schiff base made of urea and salicylaldehyde as ligand and Cu (II) and Zn (II) as metal salts.
Turner Anderson Method for determination of stability constant
Turner and Anderson [25] have modified Job's method and have successfully used for determination of stability constant. By plotting a continuous variation curve for a given range of compositions and then repeating the procedure for more dilute solutions. If the initial concentrations of the metallic ions and ligands are 'a' and 'b' respectively, then
Turner and Anderson [25] have modified Job's method and have successfully used for determination of stability constant. By plotting a continuous variation curve for a given range of compositions and then repeating the procedure for more dilute solutions. If the initial concentrations of the metallic ions and ligands are 'a' and 'b' respectively, then
Where, K = Stability Constant
X = Concentration of the complex
X = Concentration of the complex
It is assumed that Beer's Law is obeyed, i.e. the optical density of the solution is proportional to the concentration of the complex in the given range. If, therefore, any two solutions on the two curves have the same optical density, as shown in the graph a1, a2 and b1, b2 represent the concentrations of the metal and the ligand respectively on the two curves, then:
Where, the subscripts 1 and 2 refer to the reagent concentrations. Thus “K” be calculated by solving the equation.
Results and Discussion
Conductometric titration for detection of Metal-Ligand ratio (Monovariant method)
Concentration of metal = 0.01M, Concentration of ligand = 0.01M
Concentration of metal = 0.01M, Concentration of ligand = 0.01M
| Serial No. | Volume of metal salt added (ml) | Observed Conductance (µS) | Corrected Conductance (µS) |
| 1 | 0 | 81 | 81 |
| 2 | 1 | 82 | 90.2 |
| 3 | 2 | 81.9 | 98.28 |
| 4 | 3 | 81.6 | 106.08 |
| 5 | 4 | 81.2 | 113.68 |
| 6 | 5 | 80.8 | 121.2 |
| 7 | 6 | 80 | 128 |
| 8 | 7 | 79.4 | 134.98 |
| 9 | 8 | 79 | 142.2 |
| 10 | 9 | 78.6 | 149.34 |
| 11 | 10 | 78 | 156 |
| 12 | 11 | 79.1 | 166.11 |
| 13 | 12 | 79.1 | 174.02 |
| 14 | 13 | 80.9 | 186.07 |
| 15 | 14 | 82.1 | 197.04 |
| 16 | 15 | 83.7 | 209.25 |
| 17 | 16 | 85.3 | 221.78 |
| 18 | 17 | 88.6 | 239.22 |
| 19 | 18 | 90 | 252 |
| 20 | 19 | 91 | 263.9 |
| 21 | 20 | 93 | 279 |
Table 1: For Cupric Acetate salt with Schiff base (ligand).

Graph 2: Conductometric titration of Cu ion and ligand by using corrected conductance.
Graph 1 & 2: Conductometric method to determine metal: ligand ratio (Metal: Cupric acetate salt).
Graph 1 & 2: Conductometric method to determine metal: ligand ratio (Metal: Cupric acetate salt).
Determination of metal-ligand ratio (Cu: Schiff base)
V1 S1 = V2 S2
V1 S1 = V2 S2
Where, V1 = Initial volume of ligand
V2 = Volume of metal added
S1 = Strength of ligand
S2 = Strength of complex
V2 = Volume of metal added
S1 = Strength of ligand
S2 = Strength of complex
S2= 0.01 N
So that the metal ligand ratio is 0.01: 0.01 = 1: 1.
Concentration of metal= 0.01M, Concentration of ligand= 0.01M.
| Serial No. | Volume of metal salt added (ml) | Observed Conductance (µS) | Corrected Conductance (µS) |
| 1 | 0 | 81 | 81 |
| 2 | 1 | 82.4 | 90.64 |
| 3 | 2 | 82.2 | 98.64 |
| 4 | 3 | 81.1 | 105.43 |
| 5 | 4 | 84 | 117.6 |
| 6 | 5 | 84 | 126 |
| 7 | 6 | 87 | 139.2 |
| 8 | 7 | 89.7 | 152.49 |
| 9 | 8 | 90 | 162 |
| 10 | 9 | 92 | 174.8 |
| 11 | 10 | 94 | 188 |
| 12 | 11 | 96 | 201.6 |
| 13 | 12 | 98 | 215.6 |
| 14 | 13 | 100 | 230 |
| 15 | 14 | 102 | 244.8 |
| 16 | 15 | 105 | 262.5 |
| 17 | 16 | 107 | 278.2 |
| 18 | 17 | 109 | 294.3 |
| 19 | 18 | 111 | 310.8 |
| 20 | 19 | 113 | 327.7 |
| 21 | 20 | 117 | 351 |
Table 2: For Zinc Acetate salt with Schiff base (ligand).

Graph 4: Conductometric titration of Zn ion and ligand by using corrected conductance.
Graph 3 & 4: Conductometric method to determine metal: ligand ratio (Metal: Zinc acetate salt).
Graph 3 & 4: Conductometric method to determine metal: ligand ratio (Metal: Zinc acetate salt).
Determination of metal-ligand ratio (Zn: Schiff base)
V1 S1 = V2 S2
V1 S1 = V2 S2
Where, V1 = Initial volume of ligand
V2 = Volume of metal added
S1 = Strength of ligand
S2 = Strength of complex
V2 = Volume of metal added
S1 = Strength of ligand
S2 = Strength of complex
S2 = 0.03 N
So that the metal ligand ratio is 0.01: 0.03 = 1:3.
Modified Job’s Method of continuous variation for determining composition and stability constant of complex
Concentration of metal = 0.01M, Concentration of ligand = 0.01M
Concentration of metal = 0.01M, Concentration of ligand = 0.01M
| Serial No. | Ratio | M:S (C1) | S:L (C2) | M:L (C3) | ΔConductance (C1 + C2 - C3) (µS) |
Corrected Conductance (µS) |
| 1 | 00:12 | 2.39 | 80.5 | 80.7 | 2.19 | 2.19 |
| 2 | 01:11 | 4.84 | 80.8 | 81.4 | 4.24 | 4.664 |
| 3 | 02:10 | 11.8 | 80 | 81.2 | 10.6 | 12.72 |
| 4 | 03:09 | 14.9 | 78.4 | 81.7 | 11.6 | 15.08 |
| 5 | 04:08 | 21.1 | 77.6 | 83 | 15.7 | 21.98 |
| 6 | 05:07 | 26 | 77.2 | 84.5 | 18.7 | 28.05 |
| 7 | 06:06 | 31.5 | 76.2 | 86.2 | 21.5 | 34.4 |
| 8 | 07:05 | 30.3 | 74.5 | 87.1 | 17.7 | 30.09 |
| 9 | 08:04 | 34.8 | 74 | 89.5 | 17.7 | 31.86 |
| 10 | 09:03 | 36 | 71.5 | 90 | 17.1 | 29.25 |
| 11 | 10:02 | 40.8 | 71.1 | 91 | 16.9 | 30.98 |
| 12 | 11:01 | 41.5 | 69.7 | 92 | 16.6 | 31.81 |
| 13 | 12:00 | 44 | 69.2 | 94 | 16 | 32 |
Table 3: Conductance of Schiff base (ligand) and Cupric acetate.
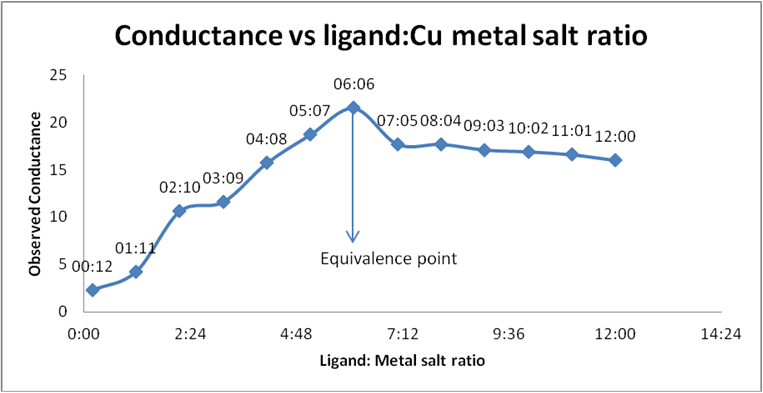
Graph 5: Conductometric estimation of composition of complex of
Schiff base (ligand) and Cu salt by using observed conductance
Concentration of metal = 0.01M, Concentration of ligand = 0.01M
| Serial No. | Ratio | M:S (C1) | S:L (C2) | M:L (C3) | ΔConductance (C1 + C2 - C3) (µS) |
Corrected Conductance (µS) |
| 1 | 00:12 | 2.71 | 80.5 | 80.7 | 2.51 | 2.51 |
| 2 | 01:11 | 6.58 | 80.8 | 81.3 | 6.08 | 6.688 |
| 3 | 02:10 | 13.2 | 80 | 81.9 | 11.3 | 13.56 |
| 4 | 03:09 | 18 | 78.4 | 81.9 | 14.5 | 18.85 |
| 5 | 04:08 | 24.8 | 77.6 | 89.4 | 13 | 18.2 |
| 6 | 05:07 | 29.7 | 77.2 | 93 | 13 | 19.5 |
| 7 | 06:06 | 32.7 | 76.2 | 96 | 12.9 | 20.64 |
| 8 | 07:05 | 37.5 | 74.5 | 101 | 11 | 18.7 |
| 9 | 08:04 | 41.5 | 74 | 103 | 10.5 | 18.9 |
| 10 | 09:03 | 45.7 | 72.6 | 107 | 10.3 | 19.57 |
| 11 | 10:02 | 51.5 | 71.1 | 110 | 10.2 | 20.4 |
| 12 | 11:01 | 56.4 | 69.7 | 113 | 10.1 | 21.21 |
| 13 | 12:00 | 59.3 | 69.2 | 116 | 10 | 22 |
Table 4: Conductance of Schiff base (ligand) and Zinc acetate.

Graph 6: Conductometric estimation of composition of complex of
Schiff base (ligand) and Zn salt by using observed conductance.
Turner Anderson Method for determination of stability constant
Concentration of metal = 0.01M, Concentration of ligand = 0.01M
Concentration of metal = 0.01M, Concentration of ligand = 0.01M
| Serial No. | Ratio | M:S (C1) | S:L (C2) | M:L (C3) | ΔConductance (C1+C2-C3) (µS) |
Corrected Conductance (µS) |
| 1 | 00:12 | 2.39 | 80.5 | 80.7 | 2.19 | 2.19 |
| 2 | 01:11 | 4.84 | 80.8 | 81.4 | 4.24 | 4.664 |
| 3 | 02:10 | 11.8 | 80 | 81.2 | 10.6 | 12.72 |
| 4 | 03:09 | 14.9 | 78.4 | 81.7 | 11.6 | 15.08 |
| 5 | 04:08 | 21.1 | 77.6 | 83 | 15.7 | 21.98 |
| 6 | 05:07 | 26 | 77.2 | 84.5 | 18.7 | 28.05 |
| 7 | 06:06 | 31.5 | 76.2 | 86.2 | 21.5 | 34.4 |
| 8 | 07:05 | 30.3 | 74.5 | 87.1 | 17.7 | 30.09 |
| 9 | 08:04 | 34.8 | 74 | 89.5 | 17.7 | 31.86 |
| 10 | 09:03 | 36 | 71.5 | 90 | 17.1 | 29.25 |
| 11 | 10:02 | 40.8 | 71.1 | 91 | 16.9 | 30.98 |
| 12 | 11:01 | 41.5 | 69.7 | 92 | 16.6 | 31.81 |
| 13 | 12:00 | 44 | 69.2 | 94 | 16 | 32 |
Table 5: Conductance of Schiff base (ligand) and cupric acetate.
Concentration of metal = 0.005M, Concentration of ligand = 0.005M
| Serial No. | Ratio | M:S (C1) | S:L (C2) | M:L (C3) | ΔConductance (C1+C2-C3) (µS) |
Corrected Conductance (µS) |
| 1 | 00:12 | 3.6 | 48.6 | 28.9 | 23.3 | 23.3 |
| 2 | 01:11 | 5.7 | 48.5 | 28.9 | 25.3 | 27.83 |
| 3 | 02:10 | 8.22 | 47.7 | 29 | 26.92 | 32.304 |
| 4 | 03:09 | 10.3 | 46.7 | 29.1 | 27.9 | 36.27 |
| 5 | 04:08 | 13 | 45.7 | 29.2 | 29.5 | 41.3 |
| 6 | 05:07 | 15.4 | 45.2 | 29.3 | 31.3 | 46.95 |
| 7 | 06:06 | 18.2 | 44.3 | 27.8 | 34.7 | 55.52 |
| 8 | 07:05 | 19.9 | 43.5 | 29.2 | 34.2 | 58.14 |
| 9 | 08:04 | 22.6 | 42.7 | 31.2 | 34.1 | 61.38 |
| 10 | 09:03 | 24.3 | 42 | 32.3 | 34 | 64.6 |
| 11 | 10:02 | 26.7 | 41.2 | 34 | 33.9 | 67.8 |
| 12 | 11:01 | 29.5 | 40.6 | 36.4 | 33.7 | 70.77 |
| 13 | 12:00 | 31.5 | 40 | 38 | 33.5 | 73.7 |
Table 6: Conductance of Schiff base (ligand) and Cupric acetate.
Stability constant calculation of Cu ion
Where, K= Stability constant
x = Concentration of complex
a = Initial concentration of metal
b = Initial concentration of ligand
x = Concentration of complex
a = Initial concentration of metal
b = Initial concentration of ligand
If, therefore, any two solutions on the two curves have the same optical density, as shown in the graph a1, a2 and b1, b2 represent the concentrations of the metal and the ligand respectively on the two curves, then:
From Graph 7,
a1 = (0.01*6)/12 = 0.005, b1 = (0.01*6)/12 = 0.005
a2 = (0.005*7)/12 = 0.00291, b2 = (0.005*5)/12 = 0.00208
a1 = (0.01*6)/12 = 0.005, b1 = (0.01*6)/12 = 0.005
a2 = (0.005*7)/12 = 0.00291, b2 = (0.005*5)/12 = 0.00208
From equation (ii),
Value of x comes out to be x = 0.00115
Value of x comes out to be x = 0.00115
Thus from equation (i)
K = 14.6828*103
logK = 4.1668
K = 14.6828*103
logK = 4.1668
Thus free energy change,
ΔG= -2.303 RT log K
ΔG= -2.303 * 8.314 * 273 * 4.1668
ΔG= -21780.5709 Kcal/mol
ΔG= -2.303 RT log K
ΔG= -2.303 * 8.314 * 273 * 4.1668
ΔG= -21780.5709 Kcal/mol
Concentration of metal = 0.01M, Concentration of ligand = 0.01M
| Serial No. | Ratio | M:S (C1) | S:L (C2) | M:L (C3) | ΔConductance (C1 + C2-C3) (µS) |
Corrected Conductance (µS) |
| 1 | 00:12 | 2.71 | 80.5 | 80.7 | 2.51 | 2.51 |
| 2 | 01:11 | 6.58 | 80.8 | 81.3 | 6.08 | 6.688 |
| 3 | 02:10 | 13.2 | 80 | 81.9 | 11.3 | 13.56 |
| 4 | 03:09 | 18 | 78.4 | 81.9 | 14.5 | 18.85 |
| 5 | 04:08 | 24.8 | 77.6 | 89.4 | 13 | 18.2 |
| 6 | 05:07 | 29.7 | 77.2 | 93 | 13 | 19.5 |
| 7 | 06:06 | 32.7 | 76.2 | 96 | 12.9 | 20.64 |
| 8 | 07:05 | 37.5 | 74.5 | 101 | 11 | 18.7 |
| 9 | 08:04 | 41.5 | 74 | 103 | 10.5 | 18.9 |
| 10 | 09:03 | 45.7 | 72.6 | 107 | 10.3 | 19.57 |
| 11 | 10:02 | 51.5 | 71.1 | 110 | 10.2 | 20.4 |
| 12 | 11:01 | 56.4 | 69.7 | 113 | 10.1 | 21.21 |
| 13 | 12:00 | 59.3 | 69.2 | 116 | 10 | 22 |
Table 7: Conductance of Schiff base (ligand) and Zinc acetate.
Concentration of metal = 0.005M, Concentration of ligand = 0.005M
| Serial No. | Ratio | M:S (C1) | S:L (C2) | M:L (C3) | ΔConductance (C1+C2-C3) (µS) |
Corrected Conductance (µS) |
| 1 | 00:12 | 1.93 | 48.6 | 27.5 | 23.03 | 23.03 |
| 2 | 01:11 | 5.23 | 48.5 | 30 | 23.73 | 26.103 |
| 3 | 02:10 | 8.3 | 47.7 | 30.8 | 25.2 | 30.24 |
| 4 | 03:09 | 10.8 | 46.7 | 31.7 | 25.8 | 33.54 |
| 5 | 04:08 | 13.2 | 45.7 | 33.2 | 25.7 | 35.98 |
| 6 | 05:07 | 15.5 | 45.2 | 35.1 | 25.6 | 38.4 |
| 7 | 06:06 | 17.1 | 44.3 | 36 | 25.4 | 40.64 |
| 8 | 07:05 | 20.4 | 43.5 | 38.6 | 25.3 | 43.01 |
| 9 | 08:04 | 22.2 | 42.7 | 39.8 | 25.1 | 45.18 |
| 10 | 09:03 | 24.3 | 42 | 41.3 | 25 | 47.5 |
| 11 | 10:02 | 26.6 | 41.2 | 42.9 | 24.9 | 49.8 |
| 12 | 11:01 | 28.4 | 40.6 | 44.3 | 24.7 | 51.87 |
| 13 | 12:00 | 30 | 40 | 45.5 | 24.5 | 53.9 |
Table 8: Conductance of Schiff base (ligand) and Zinc acetate.
Stability constant calculation of Zn ion
Where, K= Stability constant
x = Concentration of complex
a = Initial concentration of metal
b = Initial concentration of ligand
x = Concentration of complex
a = Initial concentration of metal
b = Initial concentration of ligand
If, therefore, any two solutions on the two curves have the same optical density, as shown in the graph a1, a2 and b1, b2 represent the concentrations of the metal and the ligand respectively on the two curves, then:
From Graph 8,
a1 = (0.01*6)/12 = 0.0025, b1 = (0.01*6)/12 = 0.0075
a2 = (0.005*4)/12 = 0.0016, b2 = (0.005*8)/12 = 0.0033
a1 = (0.01*6)/12 = 0.0025, b1 = (0.01*6)/12 = 0.0075
a2 = (0.005*4)/12 = 0.0016, b2 = (0.005*8)/12 = 0.0033
From equation (ii),
Value of x comes out to be x = 0.00264
Value of x comes out to be x = 0.00264
Thus from equation (i)
K = 3.5259*103
logK = 4.6878
K = 3.5259*103
logK = 4.6878
Thus free energy change,
ΔG= -2.303 RT log K
ΔG= -2.303 * 8.314 * 273 * 4.1668
ΔG= -24503.9264 Kcal/mol
ΔG= -2.303 RT log K
ΔG= -2.303 * 8.314 * 273 * 4.1668
ΔG= -24503.9264 Kcal/mol
Conclusion
Through this analysis, it has been observed that the formation of complex of Schiff base with bivalent metal cations like Cu (II) takes place in the ratio 1:1 and with Zn (II) it seems to form in the ratio of 1:3 (Monovariant method). The modified Job’s method of continuous variation was used to calculate the stability constant of the complex and the free energy change. The value of free energy change is negative showing the feasibility of complex formation. After determining the metal-ligand ratio, the stability constant and free energy changes, the complex was synthesized. Also it can be concluded that 0.01M is carrying the standard conc. for optimal complex formation.
Acknowledgement
The authors are thankful to the respected Principal Sir, Dr. Arnab Samanta, Netaji Subhas Chandra Bose Institute of Pharmacy, West Bengal for providing necessary facilities for the completion of research work.
The authors are thankful to the respected Principal Sir, Dr. Arnab Samanta, Netaji Subhas Chandra Bose Institute of Pharmacy, West Bengal for providing necessary facilities for the completion of research work.
References
- FA Cotton and G Wilkinson. "Advanced Inorganic Chemistry 4th Edtion", Wiley, London, (1980).
- W Christian. "Analytical Chemistry 3rd Edition”. Wiley, London (1980).
- H Schiff. Ann. Chem. 131: 118 (1864).
- Campbell K N. “Sommers H, Campbell B. K. J. Am. Chem. Soc”. 66: 82 (1944).
- Hine J. Yeh CY. J. Am. Chem. Soc.; 89 (1967): 2669.
- Savich IA, Pikaev AK, Lebedev IA, Spitsyn VI, Moskov vestnik. Univ. (1956): 11: 225.
- Tazoki H, Miyano K. J. chem. Soc. 97 (1959): 69.
- Robertson DN. U. S. Pat., 920.2 (1960): 101.
- Brewster CM. Am. Chem. Soc. 46 (1924): 2463.
- Munir C, Yousaf SM, Ahmed N. J. Chem. Soc. Pak. 7.4 (1985): 301.
- Brand E, Berg SM. Org. Synth. Coll. 2 (1943): 49.
- Dane E, Dress F, Konard P, Dockner T. Agnew Chem. 74 (1962): 873.
- Sheehan JC, Grenda VJ. J. Am. Chem. Soc. 84 (1962): 2417.
- Etting. C. Ann; 35: 241 (1840).
- Irving. H. and Willams. R. J. P. J. Chem. Soc; 3192 (1953).
- Yoe. J.R and A.L.Jones, Ind. Eng. Chem., Anal. Ed., 16.111 (1944).
- P. Job, Ann, Chem., 9.113 (1928).
- Vesburgh .W.R., and Cooper. G.R. J. Am. Chem. Soc; 63.437 (1941).
- Bagchi Anindya., et al. “International journal of recent advances in pharmaceutical research” 6.1 (2016): 50-58.
- Bagchi Anindya*, Mukherjee Prosenjit, Raha Anusree. UJP. 04.03 (2015): 64-69.
- Sengupta N.R., Indian Journal of Chemistry; 29.33 (1966).
- Carradona J.P. and Lippard S.J., Inorganic Chemistry; (1988).
- Huhey JE. Proceedings of the Regional Annual Chemistry Teaching Symposium; Reacts. (1973): 52-78.
- Qualitative Inorganic Analysis, Longmann Green and Co. London Vogel-I, II; (1959).
- Anderson W.F., Inorganic Chemistry in Biology and Medicine, ACS Symposium series, American Chemical Society, Washington DC; (1980).
Citation:
Anindya Bagchi., et al. “A Detailed Study of Transition Metal Complexes of a Schiff Base with Its Physico-Chemical Properties
by Using a Electrochemistry Method”. Chronicles of Pharmaceutical Science 1.3 (2017): 120-134.
Copyright: © 2017 Anindya Bagchi., et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
















































 Scientia Ricerca is licensed and content of this site is available under a Creative Commons Attribution 4.0 International License.
Scientia Ricerca is licensed and content of this site is available under a Creative Commons Attribution 4.0 International License.