Research Article
Volume 1 Issue 3 - 2017
Drugs in Binary Solvent Mixtures Their Preferential Solvation
Institute of Chemistry, Hebrew University of Jerusalem, Jerusalem 91904, Israel
*Corresponding Author: Yizhak Marcus, Institute of Chemistry, Hebrew University of Jerusalem, Jerusalem 91904, Israel.
Received: July 10, 2017; Published: July 28, 2017
Abstract
Drugs in binary solvent mixtures that are often used for their preparation or formulations are preferentially solvated by the solvent components. This phenomenon is reviewed here, based on solubility and other thermodynamic data, and as described by means of the inverse Kirkwood-Buff integrals and the quasi-lattice quasi-chemical methods. The local mole fractions of the solvent components in the solvation sphere of the drug molecule and their differences with respect to these mole fractions in the bulk, i.e., the preferential solvation parameters, relate the preferences quantitatively. When data were available at several temperatures these preferences are discussed in terms of the enthalpic and entropic contributions.
Keywords: Drugs; Binary solvent mixtures; Preferential solvation; Quasi-lattice quasi-chemical method; Inverse Kirkwood-Buff integrals method
Introduction
Drugs are generally only poorly soluble in water, and therefore co-solvents are used in order to enhance their solubility in their production processes. Many authors studied the solubilities of drugs in binary solvent mixtures extensively. These studies have been directed in many cases towards modeling the solubilities and possibly predicting them from the solubilities in the neat solvents.
One successful solubility modeling method is the ‘nearly ideal binary solvent’ (NIBS) approach of Acree and co-workers, applied to several kinds of solvent mixtures [1,2]. The modified model of Jouyban., et al. [3] has however been more appropriate in mixtures involving polar and non-polar solvents, such as water with co-solvents. Several other models have also been employed, such as those involving surface areas [4], UNIFAC group contributions [5,6], and Hildebrand solubility parameters [7-11]. Although the requirements of the pharmaceutical industry were satisfied by such studies, little insight regarding the actual molecular environment of the drug molecules in the solvent mixture was obtained in these studies. The preferential solvation of drug solutes by the components of the solvent mixtures should provide such insight.
The application of two methods, the inverse Kirkwood-Buff integrals (IKBI) method [12,13] and the quasi-lattice quasi-chemical (QLQC) one [14] to solutions of drugs in binary solvent mixtures is reviewed here. These methods present the preferential solvation of the drug molecules by the solvent components, but the exact modeling of the solubility curve is not a purpose of such studies, because the available methods [7,10,11] are adequate for this purpose. The intention is to learn something about the interactions of the solute with the solvent components surrounding its molecules from the preferential solvation.
In the following, the solute is designated by subscript S and the solvent components by subscripts A and B. The preferential solvation parameter δxA,S for the solute S expresses the results of the preferential solvation:
δxA,S = xA,SL – xA = – δxB,S (1)
δxA,S = xA,SL – xA = – δxB,S (1)
Here xA is the mole fraction of A in the bulk solvent mixture and xA,SL is its local mole fraction in the vicinity of the solute S. If δxA,S > 0 then S is preferentially solvated by A, else it is by B. Negligible preferential solvation is implied when |δxA,S| ≤ 0.01, the values are then within the error of the determination. When δxA,S. ≈ xB complete selective solvation of S by A takes place, the implication of which is that δxA,S cannot be larger than xB.
The equilibrium quotient KAB for the replacement of A molecules around the solute molecule by B ones is another way to express the preferential solvation. According to the QLQC approach, a coordination number Z is assigned to the solute; this may be composition dependent, i.e., Z(xA). The solvation numbers by the components are given by ZxA,SL for component A and Z(1– xA,SL) for B, their sum being Z. The equilibrium quotient for the replacement is
KAB = (xA,SL/xA)/[(1 – xA,SL)/(1 – xA)] (2)
KAB = (xA,SL/xA)/[(1 – xA,SL)/(1 – xA)] (2)
The summarization of the preferential solvation by a single parameter KAB is generally inexpedient, however.
Details of the Methods
The mutual interactions of the two solvents as described by the molar excess Gibbs energy of their mixing in the absence of S, GEAB, must be taken into account, because the preferential solvation of the solute S in the solvent mixture A+B depends not only on the interactions of S with A and with B, but also on these mutual interactions of the solvents. In the preferential solvation of polystyrene in mixed solvent systems [15] has this aspect already been stressed, and competitive interactions of all three components take place in the solutions.
The molar solubility data of the solute in the neat solvents and their mixture, s(S), are transformed to the standard molar Gibbs energy of transfer of S from A to A+B:
ΔtG∞(S, A → A+B) = –RTln[s(S in A+B)/s(S in A)] (3)
ΔtG∞(S, A → A+B) = –RTln[s(S in A+B)/s(S in A)] (3)
A provision is that the solute S is only sparingly soluble at all solvent compositions, concentrations are used in place of activities, solute–solute interactions may be disregarded, and the solute molecules are surrounded by solvent molecules only. Otherwise, activity coefficients of S at each solvent composition need to be employed. The identity of the solid drug that is at equilibrium with the saturated solutions being independent of the solvent composition is another provision for the application of Eq. (3), i. e., no crystal solvates are formed by the solute.
According to Marcus [16,17] the QLQC approach employs the following expressions:
xA,SL = 1/[1 + (NBB/NAA)1/2exp(ΔEAB,S/2RT)] (4)
xA,SL = 1/[1 + (NBB/NAA)1/2exp(ΔEAB,S/2RT)] (4)
The quasi-chemical aspect of the QLQC approach gives rise to Eq. (4). The lattice parameter Z in eqs. (5) to (8) arises from the quasi-lattice aspect:
NBB/NAA = [xB – NAB/Z(NA+NB)]/[xA – NAB/Z(NA+NB)] (5)
NAB/Z(NA+NB) = [1 – {1 – xAxB(1 – exp(–ΔEAB /RT))}1/2]/[2(1 – exp(–ΔEAB/RT)] (6)
exp(–ΔEAB/RT) = [{2exp(–GEAB(x = 0.5)/ZRT)} – 1]2 (7)
ΔEAB,S/RT = ΔtG∞(S, A → B)/Z (8)
NBB/NAA = [xB – NAB/Z(NA+NB)]/[xA – NAB/Z(NA+NB)] (5)
NAB/Z(NA+NB) = [1 – {1 – xAxB(1 – exp(–ΔEAB /RT))}1/2]/[2(1 – exp(–ΔEAB/RT)] (6)
exp(–ΔEAB/RT) = [{2exp(–GEAB(x = 0.5)/ZRT)} – 1]2 (7)
ΔEAB,S/RT = ΔtG∞(S, A → B)/Z (8)
The number of molecules of the solvent components in the bulk are NA and NB, whereas NAA, NBB, and NAB the numbers of neighboring pairs of these molecules on the quasi lattice. In eqs. (6) ΔEAB denotes the molar energy of interaction of molecules A and B on neighboring quasi-lattice sites, obtained from the excess Gibbs energy of mixing the components at the equimolar composition, eq. (7). In eq. (8) the difference in the molar neighbor interaction energies of S with A and B is ΔEAB,S/RT, according to the molar transfer Gibbs energy of S from neat solvent A to neat solvent B divided by Z, i.e., per neighboring lattice points. The lattice parameter Z is a fitting parameter obtained from fitting the complete ΔtG∞ = f (xA) and GEAB = f(xA) curves, but a reasonable value to use with the large drug molecules would be 10.
The local mole fractions of A around the solute molecule S, xA,SL, as a function of the solvent mixture composition are obtained from the experimental solubilities and the derived ΔtG∞(S, A → A+B) and also the GEAB of the solvents with the set of expressions (4) to (8). These, xA,SL values then yield the preferential solvation parameters δxA,S from eq, (1) and the equilibrium quotient for solvent replacement KAB from eq. (2).
Based on the original derivation by Ben–Naim [12,13], the IKBI approach has been re-cast in the following form [16,17]. The preferential solvation parameter δxA,S is obtained from the Kirkwood-Buff integrals GA,S and GB,S:
δxA,S = xAxB(GA,S – GB,S)/[ xAGA,S + xBGB,S + Vcor] (9)
δxA,S = xAxB(GA,S – GB,S)/[ xAGA,S + xBGB,S + Vcor] (9)
The Kirkwood–Buff integrals GA,S and GB,S are obtained from the thermodynamic data in eqs. (10) and (11).
GA,S = RTκT – VS + xBVBD/Q (10)
GB,S = RTκT – VS + xAVAD/Q (11)
D = d[ΔtG∞(S, A → A+B)]/dxB (12)
Q = RT + xAxB(d2GEAB/dxB2) (13)
Vcor = 2522.5[rS + 0.1363{xA,SLVA + (1– xA,SL)VB}1/3 – 0.085]3 (14)
GA,S = RTκT – VS + xBVBD/Q (10)
GB,S = RTκT – VS + xAVAD/Q (11)
D = d[ΔtG∞(S, A → A+B)]/dxB (12)
Q = RT + xAxB(d2GEAB/dxB2) (13)
Vcor = 2522.5[rS + 0.1363{xA,SLVA + (1– xA,SL)VB}1/3 – 0.085]3 (14)
The isothermal compressibility of the mixtures, κT (in GPa–1), involved in eqs. (10) and (11), is given to sufficient approximation as the linear expression xAκT(A) + xBκT(B). The partial molar volumes are VS of the solute, and VA and VB of the solvents and may be replaced to a good approximation by the molar volumes of the pure substances (in cm3 mol–1). The derivative expressions D and Q in eqs. (12) and (13) are to be obtained in kJ mol–1, as is RT.
The correlation volume around S, within which preferential solvation takes place, eq. (14), is Vcor in cm3 mol–1, the same units in which GA,S and GB,S are to be expressed . The calculation of the correlation volume requires iteration, because it depends on the local mole fractions given by eqs. (1) and (9). The radius of the solute, rS, in nm, is calculated from VS with a packing factor of 58%, according to notions in [17] and the numerical values in eq. (14) pertain to the solute with one solvation shell.
The QLQC approach is less rigorous than the IKBI one, depending on a lattice model for the solution and assumptions concerning the interactions of neighboring species. On the other hand, only the standard molar transfer energy between the neat solvents is needed for the QLQC method, contrary to the IKBI method that requires the derivative of the full ΔtG∞ = f(xA) curve. Also, for the QLQC method only the excess Gibbs energy of mixing of the equimolar solvent mixture, GEAB (x = 0.5) is needed, contrary to the IKBI method that requires the second derivative of the full GEAB = f(xA) curve. The IKBI method requires, therefore, very precise thermodynamic and solubility data for the calculation of the derivatives for the quantities D and Q, whereas the QLQC method is less demanding regarding the accuracy of the data.
Applications
This section reviews the preferential solvation of drug molecules in binary solvent mixtures obtained by the application of the QLQC and IKBI methods. The studies employed are from a single school of investigation, extending over nearly a decade, and no attempt to be exhaustive has been made. Table 1 summarizes the studies of the preferential solvation of drugs in binary solvent mixtures dealt with in this paper, whereas the details are presented following Table 1.
This section reviews the preferential solvation of drug molecules in binary solvent mixtures obtained by the application of the QLQC and IKBI methods. The studies employed are from a single school of investigation, extending over nearly a decade, and no attempt to be exhaustive has been made. Table 1 summarizes the studies of the preferential solvation of drugs in binary solvent mixtures dealt with in this paper, whereas the details are presented following Table 1.
| Drug | Solvents | Reference |
| Benzocaine | Water + ethanol, + 1,4-dioxane | 17 |
| Caffeine | Ethanol + ethyl acetate | 17 |
| Diazepam | Water + ethanol, + 1,4-dioxane | 17 |
| Etoricoxib | Water + ethanol, + 1,4-dioxane, + 1,4-butanediol, + dimethyl-formamide, + dimethylacetamide, + dimethyl sulfoxide | 39 |
| Ibrutinib | Water + ethanol | 40 |
| Ibrutinib | Water + 2-ethoxy-(2-ethoxy)ethanol | 41 |
| Ibuprofen | Water + 1,2-propanediol | 25 |
| Ibuprofen | Water + methanol | 38 |
| Indomethacine | Water + 1,4-dioxane | 31 |
| Indomethacine | Ethanol + ethyl acetate | 32 |
| Ketoprofen | Water + methanol | 38 |
| Meloxicam | Water + methanol | 28 |
| Meloxicam | Water + ethanol | 29 |
| Meloxicam | Water + 1,4-dioxane | 30 |
| Meloxicam | Water + 1,2-propanediol | 26 |
| Meloxicam | Ethanol + ethyl acetate | 27 |
| Methocarbamol | Water + methanol, + ethanol, + 1,4-dioxane, + 1,2-propanediol | 33 |
| Naldixic acid | Water + 1,4-dioxane | 17 |
| Naproxen | Water + 1,2-propanediol | 25 |
| Naproxen | Ethanol + ethyl acetate | 33 |
| Naproxen | Water + methanol | 38 |
| Niflumic acid | Ethanol + ethyl acetate | 17 |
| Paracetamol | Water + 1,4-dioxane | 17 |
| Phenacetine | Water + 1,4-dioxane | 17 |
| Sulfadiazine | Water + methanol | 34 |
| Sulfadiazine | Water + 1,4-dioxane | 37 |
| Sulfamerazine | Water + methanol | 35 |
| Sulfamethazine | Water + methanol | 36 |
Table 1: Summary of the drugs and binary solvent mixtures dealt with here.
Both the QLQC and IKBI approaches could be employed with congruous results regarding the solubilities of caffeine and niflumic acid in mixtures of ethyl acetate and ethanol [18], with data taken from Bustamante., et al. [19]. Figure. 1 shows the resulting preferential solvation parameter of the drugs by the ethanol component, as a function of the ethanol mole fraction. Both drugs prefer ethanol at lower contents of this protic component but ethyl acetate at higher ones.
Differences in the results from the IKBI and QLQC approaches were obtained by Marcus [17], however, when the solubilities of caffeine and niflumic acid in mixtures of water with ethanol [19] were examined. Although the results are in agreement qualitatively, the shapes of the curves and the positions of the maxima differ. Both methods show that ethanol is preferred by the niflumic acid over water in its near environment at all solvent compositions, but caffeine prefers ethanol in its environment over water only at low ethanol contents, and at high ones water is somewhat preferred.
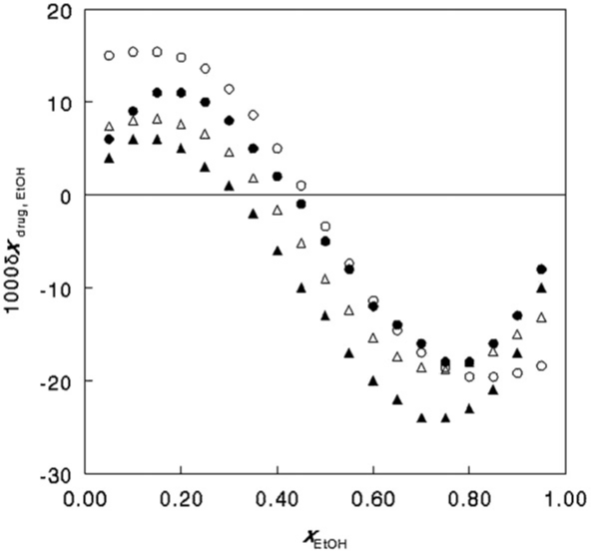
Figure 1: The preferential solvation parameter for the solvation of niflumic acid (circles) and caffeine (triangles) by the ethanol in mixtures of ethyl acetate and ethanol, as obtained by the QLQC (filled symbols) and IKBI (empty symbols) approaches. From ref. [17] by permission of Elsevier.
The solubilities of diazepam and benzocaine in mixtures of water and ethanol were measured by Rubino and Yalkowski [20] and preference of ethanol over water is exhibited by both methods. This preference is somewhat larger for diazepam than for benzocaine, but the positions of the maxima in δxS,EtOH differ [17]. The solubilities of these two drugs were also measured by Rubino and coworkers in mixtures of water with 1,4-dioxane (DX) [21]. The QLQC method leads to preference for dioxane over water over the entire composition range [17], but the IKBI method produces an unexplained break in the curve near the solvent equimolar composition for benzocaine. This break results from the shape of the derivative of the Gibbs energy of transfer data, ΔtG∞(S, A → A+B), that were obtained from the solubility ratios [21], and as explained in [17] arises from lack of data in the range xDX > 0.65,.
Bustamante and coworkers [22,23] reported the solubilities of paracetamol, phenacetin, and nalidixic acid in mixtures of water with 1,4-dioxane and the preference of these drugs for dioxane derived from both the IKBI and QLQC approaches increases in the listed order [17].
Manrique., et al. [24] reported the solubilities of the ibuprofen and naproxen in mixtures of water and 1,2-propylene glycol (PG), and that of ibuprofen is considerable at the higher temperatures, but no activity coefficient data are available needed for dealing with solute-solute interactions. The excess Gibbs energies of mixing have not been reported for the water + PG system, but such values can be derived from published water activities data. This was shown by Marcus [25], where also the manners of obtaining the necessary thermodynamic data for the application of the IKBI method are reported. Propylene glycol (PG) is preferred over water in the surroundings of both drug molecules, of ibuprofen more than of naproxen, although the preference is not large, as indicated by Both the QLQC and IKBI methods.
The preferences increases somewhat with increasing temperatures. Whereas ibuprofen has the carboxylic group as a hydrophilic head and a hydrophobic tail, naproxen has in addition to the hydrophilic carboxylic acid head also a methoxy group in the hydrophobic tail, which is albeit more bulky.
Water has a more pronounced and stiff network of hydrogen bonds than PG, hence neat PG solvates both drugs many times better than water does. The molecules of the solvent components interact more strongly with each other than with their own kind, as shown by the negative excess Gibbs energy Gwater,PGE values. This interaction loosens the tight hydrogen bond network of the water and facilitates the inclusion of the drug molecules, in addition to the direct solvation of the polar groups. The result is a preferential solvation of both drug molecules, ibuprofen and naproxen, by PG at all compositions, but not as much as would have been suggested by the differences in the solvation abilities of the neat solvent components [25].
A large body of information concerning the preferential solvation of drugs in binary solvent mixtures is due to the school of investigations involving Martinez and co-workers in Colombia. Holguin., et al. [26] measured the solubility of meloxicam in aqueous PG mixtures at several temperatures from 20 to 40°C and its preferential solvation was derived by the IKBI method. The solubility diminished strongly from that in neat propylene glycol to that in pure water at all the temperatures studied. For the propylene glycol-rich mixtures the driving mechanism for meloxicam solubility was the enthalpy, due to better solvation of the drug, whereas in the water-rich mixtures it was the entropy, due to water-structure loss around nonpolar moieties of the drug. At all compositions rather small preferential solvation of meloxicam by propylene glycol was observed.
The preferential solvation of meloxicam was also studied in four other solvent mixtures: in mixtures of ethanol and ethyl acetate (EA) [27], of water and methanol [28], of water and ethanol [29], and of water with 1,4-dioxane (DX) [30]. The mixtures of ethanol and ethyl acetate involved the equilibrium solubility of meloxicam at five temperatures from 20 to 40°C. The IKBI method was used for the derivation of the preferential solvation parameters of the drug, that for ethyl acetate is δxS,EA < 0 in ethanol-rich mixtures but > 0 at 0.38 < xEA < 0.80.
The interaction by acidic hydrogen-bonding by ethanol on the basic sites of meloxicam plays a relevant role in the drug solvation in the ethanol-rich region. In ethyl acetate-rich mixtures the slight preference of this drug for ethanol was explained in terms of the common participation of basic sites in both solvents and/or the acidic site of ethanol with the respective counterparts of meloxicam [27].
Figure 2 shows the preferential solvation parameters δxS,A values for meloxicam in several binary aqueous mixtures with co-solvents at 25⁰C obtained by the IKBI method. All the curves show preferential solvation by water (solvent B) in water-rich mixtures, δxS,A < 0, and preferential solvation by the co-solvent (solvent A), δxS,A > 0, at the intermediate compositions up to the neat co-solvent, except that ethanol has δxS,A < 0 at the ethanol-rich compositions, which fact is not readily understood. The diverging values for aqueous dioxane are due to the apparent divergence observed in the GS,water integrals due to the large negative values of D in eq. (12).
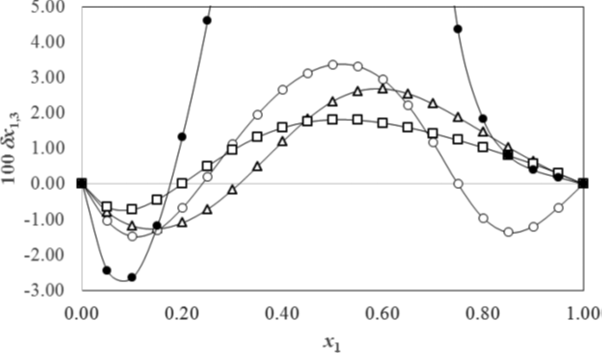
Figure 2: The preferential solvation δx1,3 (δxsolvent 1,,solute) of meloxicam in aqueous/co-solvent
mixtures. Solvent 1 is: ● 1,4-dioxane, Δ methanol, o ethanol, and □ propylene glycol. Reprinted
with permission from ref. [30] Copyright 2014 American Chemical Society
Ruidiaz., et al. [31] applied both the QLQC and the IKBI methods to the solubility of indomethacine in mixtures of water with 1,4-dioxane (DX) at several temperatures between 20 and 40⁰C. Hydrogen bonding of the carboxylate group of indomethacine to the more basic solvent component, 1,4-dioxane, causes the latter to solvate the drug molecules preferentially, but the strong self-interaction of the water molecules hinders the introduction of the bulky drug molecules into this network too. Entropy-driving takes place for the solution processes up to 0.60 mass fraction of 1,4-dioxane, whereas, beyond this proportion enthalpy-driving occurs.
The preferential solvation parameters of indomethacin in ethyl acetate (EA) + ethanol mixtures were obtained by Rodríguez., et al. [32] by means of the inverse Kirkwood–Buff integrals method. The preferential solvation parameter for ethyl acetate, δxS,EA, is positive in compositions from 0.36 < xEA < 0.71, but is negative in ethanol-rich and ethyl acetate-rich mixtures. In ethanol-rich mixtures, the acidic interaction of ethanol on basic sites of the drug plays a relevant role in the solvation. The better solvation by ethyl acetate in mixtures of comparable compositions of the two solvents was attributed to polarity effects. The slight preference of the drug for ethanol in ethyl acetate-rich mixtures was attributed to the participation of basic sites in both solvents and the acidic site of the drug. Naproxen was found to behave in these solvent mixtures in the same manner as indomethacine [32].
Jiménez., et al. [33] derived the preferential solvation of methocarbamol in a series of mixtures consisting of water (B) with each of the co-solvents dioxane, ethanol, methanol, and propylene glycol (A) from their thermodynamic properties by using the IKBI method. The preferential solvation parameter δxS,A is negative in water-rich and co-solvent-rich mixtures, but positive in mixtures with similar proportions of solvents. An exception is methanol + water mixtures, where positive values are found in the methanol-rich mixtures. The hydrophobic hydration around the non-polar groups in water-rich mixtures plays a relevant role. Whereas in co-solvent-rich mixtures the preferential solvation by water is attributed to the acidic nature of water, the drug is mainly solvated by the co-solvent in mixtures of similar solvent compositions due to the basic sites of the co-solvents.
Recent studies dealt with the preferential solvation of several sulfa-drugs in solvent mixtures: the solubility of sulfadiazine [34], sulfamerazine [35], and sulfamethazine [36] in methanol + water mixtures was measured at five temperatures from 20 to 40°C. The driving mechanism for dissolution of these drugs in water-rich mixtures was the entropy, but from the mass fraction wMeOH = 0.20 (from wMeOH = 0.70 in the case of sulfamethazine) up to neat methanol the process was enthalpy-driven, and a non-linear enthalpy–entropy relationship was observed.
Analysis by means of the IKBI method of the preferential solvation of these drugs by the solvents indicated that they were preferentially solvated by water in water-rich mixtures but preferentially solvated by methanol in methanol-rich mixtures. The driving mechanism for the dissolution process of sulfadiazine in 1,4-dioxane +water mixtures [37] was the enthalpy at nearly all the solvent compositions. Sulfadiazine was preferentially solvated by water in water-rich and in 1,4-dioxane-rich mixtures but preferentially solvated by 1,4-dioxane in those mixtures with intermediate compositions, as obtained by means of the IKBI method.
The solubilities of several anti-inflammatory drugs: naproxen, ketoprofen, and ibuprofen in methanol + water binary mixtures at 25°C yielded their preferential solvation parameters by means of the IKBI method [38]. These drugs are very sensitive to specific solvation effects. The preferential solvation parameters by methanol δxS,MeOH are positive at compositions from xMeOH = 0.32 up to pure methanol, but negative in water-rich mixtures. In the latter region the hydrophobic hydration around aromatic rings and/or methyl groups plays a dominant role in the solvation. The higher solvation by methanol at xMeOH > 0.32 was explained in terms of the higher basicity of methanol interacting with the hydroxyl group of the drugs.
Preferential solvation parameters of etoricoxib in several solvent mixtures involving 1,4-dioxane, N,N-dimethylacetamide, 1,4-butanediol, N,N-dimethylformamide, ethanol, and dimethyl sulfoxide (solvent A) with water (solvent B) were calculated from solubilities and other thermodynamic data by the IKBI method [39]. Etoricoxib was preferentially solvated by water, δxS,A < 0, in water-rich and co-solvent-rich mixtures, but in mixtures with similar proportions of both solvents δxS,A > 0 was found. Hydrophobic hydration played a dominant role in the drug solvation in water-rich mixtures. In mixtures of similar solvent proportions the drug acted as a Lewis acid with the more basic co-solvents. In co-solvent-rich mixtures the preferential solvation by water was due to the relatively higher acidity of the water. No relation between preferential solvation magnitude and co-solvent polarities was observed.
The preferential solvation of the anti-cancer drug ibrutinib in mixtures of ethanol and water [40] and of 2-(2-ethoxy) ethoxyethanol and water [41] was studied by means of the inverse IKBI method. Addition of ethanol (A) to water (B) yields negative δxS,A values up to the mixture with xEtOH = 0.24 reaching minimum values at xEtOH = 0.10. Hydrophobic hydration in these water-rich mixtures around the non-polar groups of ibrutinib contributes to lowering the δxS,A to negative values. When 0.24 < xEtOH < 1.00, the δxS,A values are positive on the other hand. The action of the co-solvent to increase the solubility of ibrutinib was related to the breaking of the ordered structure of water around the non-polar moieties of the solute and also to the fact that ibrutinib was acting as a Lewis acid with ethanol that is more basic than water. The preferential solvation by ethanol diminishes with increasing temperatures as has been also been reported for some sulfonamides in these solvent mixtures [35]. The behavior of ibrutinib in mixtures of 2-(2-ethoxy) ethoxyethanol (A) and water (B) [41] is similar to that in aqueous ethanol, except that a sharp minimum of δxS,A occurs at xA = 0.05 and this quantity becomes positive at xA > 0.15.
Discussion
Few investigations other than those summarized above deal directly with the preferential solvation of drug molecules in binary solvent mixtures, and these employ neither the QLQC nor the IKBI method. Shehatta [42] related deviations from the linear solvation energy relationships observed in aqueous ethanol mixtures with several solvatochromic indicators to those observed with the drug Trazodone. A more recent study by Boroujeni and Gharib [43] involved the drug Deferiprone as the solvatochromic probe in several aqueous co-solvent mixtures: with methanol, ethanol, 2-propanol, 1-propanol, acetonitrile, and dioxane.
The preferential solvation of drugs in binary solvent mixtures involves the QLQC and mainly the IKBI methods as the major means to obtain this information in a large body of studies, however. These investigations dealt with solutions of a large variety of drugs in mixtures of bio-compatible solvents mainly with water, but not exclusively. The presence of acidic (hydrogen bond donating) sites and/or basic (hydrogen bond accepting) sites on the drug molecules determines the solvation of the drug by basic and respectively acidic solvents, relating to the enthalpic aspect of its solubilization. The accommodation of the bulky drug molecules in the hydrogen-bonded network of water is another contribution to this aspect, in particular pertaining to the aqueous component of the solvent mixture. On the other hand, the entropic aspect involves the release of solvent molecules from such networks to become freely moving particles. These modes of interaction dictate the final picture of the preferential solvation, as is illustrated in Figures 1 and 2.
Conclusions
Binary solvent mixtures are useful for the production, separation, and formulation of drugs, since drugs are generally only sparingly soluble in the solvent of physiological importance: water. Although many models have been proposed for the description and eventual prediction of the solubility of drugs in binary solvent mixtures, these may not contribute to the understanding of the interactions of the drug molecules with the solvent components (and of these among themselves). However, such an understanding is essential for a better ability of the selection of suitable co-solvents. The QLQC and IKBI methods described in this review contribute strongly to this understanding of the preferential solvation of the drug molecules by the solvent components. Both the enthalpic and the entropic aspects of the dissolution of the drugs in the binary solvent mixtures can be derived from these studies, carried out at several temperatures.
References
- Acree WE Jr and Rytting JH. “Solubility in binary solvent systems. I: Specific versus nonspecific interactions”. Journal of Pharmaceutical Sciences 71.2 (1982): 201-205.
- Jouyban Gharasmaleki A., et al. “Comparison of various cosolvency models for calculating solute solubility in water–cosolvent mixtures”. International Journal of Pharmaceutics 177.1 (1999): 93-101.
- Jouyban A., et al. “Predicting solubility of anthracene in non-aqueous solvent mixtures using a combination of Jouyban-Acree and Abraham models”. Chemical and Pharmaceutical Bulletin 54.8 (2006): 1124-1130.
- Acree WE Jr and Rytting JH. “Solubility in binary solvent systems. III: Predictive expressions based on molecular surface areas”. Journal of Pharmaceutical Sciences 72.3 (1983): 292-296.
- Acree WE Jr and Rytting JH. “Solubility in binary solvent systems. IV. Prediction of naphthalene solubilities using the LJNIFAC group contribution mode”. International Journal of Pharmaceutics 13.2 (1983): 197-204.
- Subrahmanyam CVS and Sarasija S.” Solubility behavior of carbamazepine in binary solvents. Extended Hildebrand solubility approach to obtain solubility and other parameters”. Pharmazie 52 (1997): 939-942.
- Martin A., et al. “Extended Hildebrand solubility approach: solubility of theophylline in polar binary solvents”. Journal of Pharmaceutical Sciences 69.5 (1980): 487-491.
- Martin A and Miralles MJ. “Extended Hildebrand solubility approach: solubility of tolbutamide, acetohexamide, and sulfisomidine in binary solvent mixtures”. Journal of Pharmaceutical Sciences 71.4 (1982): 439-442.
- Pena MA., et al. “Pharmaceutical nanotechnology: solubility parameter of drugs for predicting the solubility profile type within a wide polarity range in solvent mixtures”. International Journal of Pharmaceutics 321.1-2 (2006): 155–161.
- Acree WE Jr and Tucker SA. “Thermochemical investigations of hydrogen-bonded solutions Part 6. Comparison of mobile order theory versus Kretschmer-Wiebe association model for describing anthracene solubilities in binary hydrocarbon + alcohol solvent mixtures”. Fluid Phase Equilibria 102.1 (1994): 17-29.
- Ruckenstein E and Shulgin IL. “Solubility of drugs in aqueous solutions Part 1. Ideal mixed solvent approximation”. International Journal of Pharmaceutics 258.1-2 (2003): 193-201.
- Ben-Naim A. “Theory of preferential solvation of nonelectrolytes”. Cell Biophysics 12 (1988): 255-269.
- Ben-Naim A. “Preferential solvation in two- and in three-component systems”. Pure and Applied Chemistry 62.1 (1990): 25-34.
- Marcus Y. “A quasi-lattice quasi-chemical theory of preferential solvation of ions”. Australian Journal of Chemistry 36 (1983): 1719-1738.
- Aminabhavi TM and Munk P. “Preferential adsorption onto polystyrene in mixed solvent systems”. Macromolecules 12.4 (1979): 607-613.
- Marcus Y. “Solvent Mixtures. Properties and Preferential Solvation”. M. Dekker, New York (2002): 258.
- Marcus Y. “On the preferential solvation of drugs and PAHs in binary solvent mixtures”. Journal of Molecular Liquids 140.1-3 (2008): 61-67.
- Marcus Y. “The sizes of molecules – revisited”. Journal of Physical Organic Chemistry 16.7 (2003): 398-408.
- Bustamante P., et al. “Thermodynamic origin of the solubility profile of drugs showing one or two maxima against the polarity of aqueous and nonaqueous mixtures: niflumic acid and caffeine”. Journal of Pharmaceutical Sciences 91.3 (2002): 874-883.
- Rubino JT and Yalkowsky SH. “Solubilization by cosolvents. III: diazepam and benzocaine in binary solvents”. Journal of Parenteral Science and Technology 39.3 (1985): 106-111.
- Rubino JT., et al. “Solubilization by cosolvents IV: benzocaine, diazepam and phenytoin in aprotic cosolvent-water mixtures”. Journal of Parenteral Science and Technology 41.5 (1987) 172-176.
- Bustamante C and Bustamante P. “Nonlinear enthalpy-entropy compensation for the solubility of phenacetin in dioxane-water solvent mixtures”. Journal of Pharmaceutical Sciences 85.10 (1996): 1109-1111.
- Bustamante P., et al. “Enthalpy-entropy compensation for the solubility of drugs in solvent mixtures: paracetamol, acetanilide, and nalidixic acid in dioxane-water”. Journal of Pharmaceutical Sciences 87.12 (1998): 1590-1596.
- Manrique YJ., et al. “ Thermodynamics of Mixing and Solvation of Ibuprofen and Naproxen in Propylene Glycol + Water Cosolvent Mixtures”. Journal of Solution Chemistry 37.2 (2008): 165–181.
- Marcus Y. “Preferential solvation of ibuprofen and naproxen in aqueous 1, 2-propanediol”. Acta Chimica Slovenica 56 (2009): 40-44.
- Holguín AR., et al. “Solution thermodynamics and preferential solvation of meloxicam in propylene glycol + water mixtures”. Journal of Solution Chemistry 40.12 (2011): 1987–1999.
- Cristancho DM and Martínez F. “Solubility and preferential solvation of meloxicam in ethyl acetate + ethanol mixtures at several temperatures”. Journal of Molecular Liquids 200 (2014): 122–128.
- Delgado DR., et al. “Solubility and preferential solvation of meloxicam in methanol + water mixtures at 298.15 K”. Journal of Molecular Liquids 197 (2014): 368–373.
- Delgado DR., et al. “Solubility and preferential solvation of meloxicam in ethanol + water mixtures”. Fluid Phase Equilibria 305.1 (2011): 88-95.
- Jiménez DM., et al. “Solubility and solution thermodynamics of meloxicam in 1, 4-dioxane and water mixtures”. Industrial & Engineering Chemistry Research 53.42 (2014): 16550−16558.
- Ruidiaz MA., et al. “Solubility and preferential solvation of indomethacin in 1, 4-dioxane + water solvent mixtures”. Fluid Phase Equilibria 299.2 (2010): 259-265.
- Rodríguez GA., et al. “Preferential solvation of indomethacin and naproxen in ethyl acetate + ethanol mixtures according to the IKBI method”. Physics and Chemistry of Liquids 52.4 (2014): 533–545.
- Jiménez DM., et al. “Preferential solvation of methocarbamol in aqueous binary co-solvent mixtures at 298.15 K”. Physics and Chemistry of Liquids 52.6 (2014): 726-737.
- Delgado DR and Martínez F. “Solubility and preferential solvation of sulfadiazine inmethanol + water mixtures at several temperatures”. Fluid Phase Equilibria 379 (2014): 128–138.
- Delgado DR and Martınez F. “Solution thermodynamics and preferential solvation of sulfamerazine in methanol + water mixtures”. Journal of Solution Chemistry 44.2 (2015): 360–377.
- Delgado DR., et al. “Solution thermodynamics and preferential solvation of sulfamethazine in (methanol + water) mixtures”. The Journal of Chemical Thermodynamics 97 (2016): 264–276.
- Jiménez DM., et al. “Solubility temperature dependence and preferential solvation of sulfadiazine in 1, 4-dioxane +water co-solvent mixtures”. Fluid Phase Equilibria 397 (2015): 26–36.
- Jiménez DM., et al. “Solubility and preferential solvation of some nonsteroidal anti-inflammatory drugs in methanol + water mixtures at 298.15 K”. Physics and Chemistry of Liquids 54.6 (2016): 686–702.
- Martínez F., et al. “Preferential solvation of etoricoxib in some aqueous binary cosolvent mixtures at 298.15 K”. Physics and Chemistry of Liquids 55.3 (2016): 291-303.
- Martínez F., et al. “Further numerical analysis on the solubility of ibrutinib in ethanol + water mixtures at different temperatures”. Journal of Molecular Liquids 218 (2016): 35–38.
- Martínez F., et al. “Comments on ‘‘Solubility and thermodynamic function of a new anticancer drug ibrutinib in {2-(2-ethoxyethoxy) ethanol + water} mixtures at different temperatures”. The Journal of Chemical Thermodynamics 95 (2016): 180–182.
- Shehatta. “Effect of preferential solvation on the thermodynamic properties of antidepressant drug trazodone in aqueous ethanol: linear free-energy relationships”. Helvetica Chimica Acta 85.7 (2002): 2125-2167.
- Boroujeni HC and Gharib F. “Solvatochromism and preferential solvation of deferiprone in some water–organic mixed solvents”. Journal of Solution Chemistry 45.1 (2016): 95–108.
Citation:
Yizhak Marcus. “Drugs in Binary Solvent Mixtures Their Preferential Solvation”. Chronicles of Pharmaceutical Science 1.3
(2017): 149-159.
Copyright: © 2017 Yizhak Marcus. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.































 Scientia Ricerca is licensed and content of this site is available under a Creative Commons Attribution 4.0 International License.
Scientia Ricerca is licensed and content of this site is available under a Creative Commons Attribution 4.0 International License.